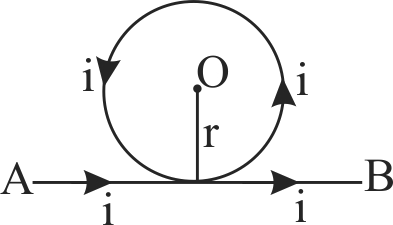
362531 Two similar coils of radius \(R\) and number of turns \(N\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(I\,\& \,I\sqrt 3 \) respectively. Find the magnetic field induction at the center of the coils.
362532
In the given figure, magnetic field at the center of ring \({(O)}\) is \({8 \sqrt{2} T}\). Now, it is turned through a \({90^{\circ}}\) angle about \({x x^{\prime}}\) axis, so that two semicircular parts are mutually perpendicular. Find the value of magnetic field (in \(T\,)\) at centre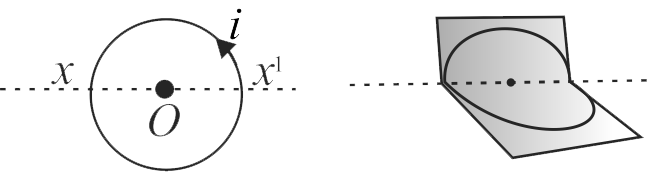
362534 Two concentric coils each of radius equal to \(2\,\pi \,cm\) are placed at right angles to each other. \(3\;A\) and \(4\;A\) are the current flowing in each coil, respectively. The magnetic induction (in \(Wb{m^{ - 2}}\)) at the centre of the coils will be (Take, \({\mu _0} = 4\pi \times {10^{ - 7}}\;Wb\,{A^{ - 1}}\;{m^{ - 1}}\)).
362535 Two identical wires \(A\) and \(B\), each of length ' \(\ell\) ', carry the same current \(I\). Wire \(A\) is bent into a circle of radius \(R\) and wire \(B\) is bent to form a square of side ' \(a\) '. If \(B_{A}\) and \(B_{B}\) are the values of magnetic field at the centers of the circle and square respectively, then the ratio \(\dfrac{B_{A}}{B_{B}}\) is
362531 Two similar coils of radius \(R\) and number of turns \(N\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(I\,\& \,I\sqrt 3 \) respectively. Find the magnetic field induction at the center of the coils.
362532
In the given figure, magnetic field at the center of ring \({(O)}\) is \({8 \sqrt{2} T}\). Now, it is turned through a \({90^{\circ}}\) angle about \({x x^{\prime}}\) axis, so that two semicircular parts are mutually perpendicular. Find the value of magnetic field (in \(T\,)\) at centre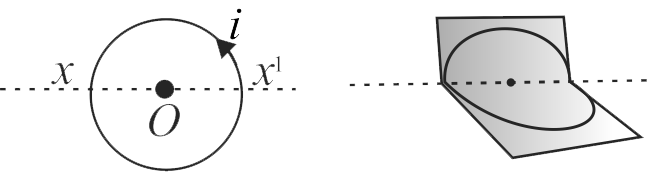
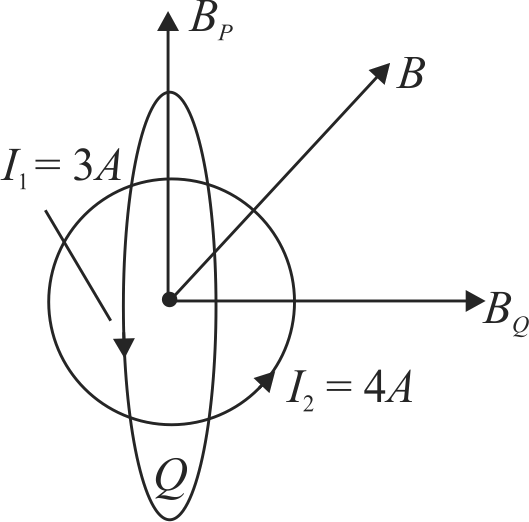
362534 Two concentric coils each of radius equal to \(2\,\pi \,cm\) are placed at right angles to each other. \(3\;A\) and \(4\;A\) are the current flowing in each coil, respectively. The magnetic induction (in \(Wb{m^{ - 2}}\)) at the centre of the coils will be (Take, \({\mu _0} = 4\pi \times {10^{ - 7}}\;Wb\,{A^{ - 1}}\;{m^{ - 1}}\)).
362535 Two identical wires \(A\) and \(B\), each of length ' \(\ell\) ', carry the same current \(I\). Wire \(A\) is bent into a circle of radius \(R\) and wire \(B\) is bent to form a square of side ' \(a\) '. If \(B_{A}\) and \(B_{B}\) are the values of magnetic field at the centers of the circle and square respectively, then the ratio \(\dfrac{B_{A}}{B_{B}}\) is
362531 Two similar coils of radius \(R\) and number of turns \(N\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(I\,\& \,I\sqrt 3 \) respectively. Find the magnetic field induction at the center of the coils.
362532
In the given figure, magnetic field at the center of ring \({(O)}\) is \({8 \sqrt{2} T}\). Now, it is turned through a \({90^{\circ}}\) angle about \({x x^{\prime}}\) axis, so that two semicircular parts are mutually perpendicular. Find the value of magnetic field (in \(T\,)\) at centre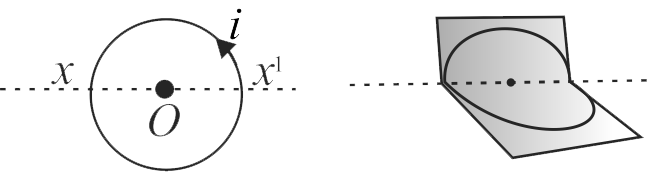
362534 Two concentric coils each of radius equal to \(2\,\pi \,cm\) are placed at right angles to each other. \(3\;A\) and \(4\;A\) are the current flowing in each coil, respectively. The magnetic induction (in \(Wb{m^{ - 2}}\)) at the centre of the coils will be (Take, \({\mu _0} = 4\pi \times {10^{ - 7}}\;Wb\,{A^{ - 1}}\;{m^{ - 1}}\)).
362535 Two identical wires \(A\) and \(B\), each of length ' \(\ell\) ', carry the same current \(I\). Wire \(A\) is bent into a circle of radius \(R\) and wire \(B\) is bent to form a square of side ' \(a\) '. If \(B_{A}\) and \(B_{B}\) are the values of magnetic field at the centers of the circle and square respectively, then the ratio \(\dfrac{B_{A}}{B_{B}}\) is
362531 Two similar coils of radius \(R\) and number of turns \(N\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(I\,\& \,I\sqrt 3 \) respectively. Find the magnetic field induction at the center of the coils.
362532
In the given figure, magnetic field at the center of ring \({(O)}\) is \({8 \sqrt{2} T}\). Now, it is turned through a \({90^{\circ}}\) angle about \({x x^{\prime}}\) axis, so that two semicircular parts are mutually perpendicular. Find the value of magnetic field (in \(T\,)\) at centre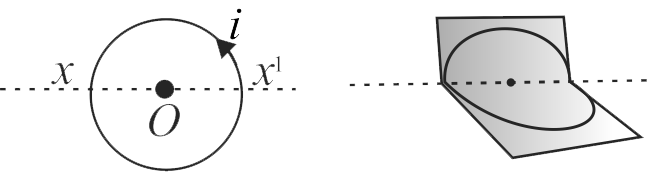
362534 Two concentric coils each of radius equal to \(2\,\pi \,cm\) are placed at right angles to each other. \(3\;A\) and \(4\;A\) are the current flowing in each coil, respectively. The magnetic induction (in \(Wb{m^{ - 2}}\)) at the centre of the coils will be (Take, \({\mu _0} = 4\pi \times {10^{ - 7}}\;Wb\,{A^{ - 1}}\;{m^{ - 1}}\)).
362535 Two identical wires \(A\) and \(B\), each of length ' \(\ell\) ', carry the same current \(I\). Wire \(A\) is bent into a circle of radius \(R\) and wire \(B\) is bent to form a square of side ' \(a\) '. If \(B_{A}\) and \(B_{B}\) are the values of magnetic field at the centers of the circle and square respectively, then the ratio \(\dfrac{B_{A}}{B_{B}}\) is
362531 Two similar coils of radius \(R\) and number of turns \(N\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(I\,\& \,I\sqrt 3 \) respectively. Find the magnetic field induction at the center of the coils.
362532
In the given figure, magnetic field at the center of ring \({(O)}\) is \({8 \sqrt{2} T}\). Now, it is turned through a \({90^{\circ}}\) angle about \({x x^{\prime}}\) axis, so that two semicircular parts are mutually perpendicular. Find the value of magnetic field (in \(T\,)\) at centre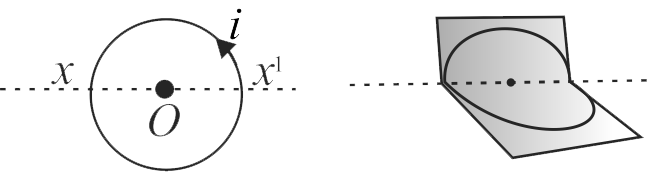
362534 Two concentric coils each of radius equal to \(2\,\pi \,cm\) are placed at right angles to each other. \(3\;A\) and \(4\;A\) are the current flowing in each coil, respectively. The magnetic induction (in \(Wb{m^{ - 2}}\)) at the centre of the coils will be (Take, \({\mu _0} = 4\pi \times {10^{ - 7}}\;Wb\,{A^{ - 1}}\;{m^{ - 1}}\)).
362535 Two identical wires \(A\) and \(B\), each of length ' \(\ell\) ', carry the same current \(I\). Wire \(A\) is bent into a circle of radius \(R\) and wire \(B\) is bent to form a square of side ' \(a\) '. If \(B_{A}\) and \(B_{B}\) are the values of magnetic field at the centers of the circle and square respectively, then the ratio \(\dfrac{B_{A}}{B_{B}}\) is