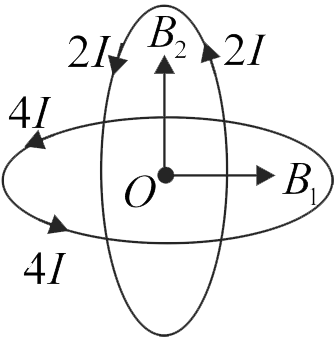
362566 Two similar coils of radius \(R\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(21\) and \(41\) respectively. The resultant magnetic field induction at the centre is found to be \(N\) times \(\frac{{{\mu _0}I}}{R}\). Find the value of \(N\) is (Take \(\sqrt{5}=2.24\) )
362566 Two similar coils of radius \(R\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(21\) and \(41\) respectively. The resultant magnetic field induction at the centre is found to be \(N\) times \(\frac{{{\mu _0}I}}{R}\). Find the value of \(N\) is (Take \(\sqrt{5}=2.24\) )
362566 Two similar coils of radius \(R\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(21\) and \(41\) respectively. The resultant magnetic field induction at the centre is found to be \(N\) times \(\frac{{{\mu _0}I}}{R}\). Find the value of \(N\) is (Take \(\sqrt{5}=2.24\) )
362566 Two similar coils of radius \(R\) are lying concentrically with their planes at right angles to each other. The currents flowing in them are \(21\) and \(41\) respectively. The resultant magnetic field induction at the centre is found to be \(N\) times \(\frac{{{\mu _0}I}}{R}\). Find the value of \(N\) is (Take \(\sqrt{5}=2.24\) )