362572
\(A\) and \(B\) are the two concentric circular conductors of center \(O\) and carrying currents \(I_{1}\) and \(I_{2}\) as shown in the adjacent figure. If ratio of their radii is \(1: 2\) and ratio of the flux densities at \(O\) due to \(A\) and \(B\) is \(1: 3\) then the value of \(I_{1} /\) \(I_{2}\) is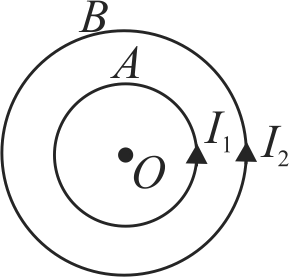
362572
\(A\) and \(B\) are the two concentric circular conductors of center \(O\) and carrying currents \(I_{1}\) and \(I_{2}\) as shown in the adjacent figure. If ratio of their radii is \(1: 2\) and ratio of the flux densities at \(O\) due to \(A\) and \(B\) is \(1: 3\) then the value of \(I_{1} /\) \(I_{2}\) is
362572
\(A\) and \(B\) are the two concentric circular conductors of center \(O\) and carrying currents \(I_{1}\) and \(I_{2}\) as shown in the adjacent figure. If ratio of their radii is \(1: 2\) and ratio of the flux densities at \(O\) due to \(A\) and \(B\) is \(1: 3\) then the value of \(I_{1} /\) \(I_{2}\) is
362572
\(A\) and \(B\) are the two concentric circular conductors of center \(O\) and carrying currents \(I_{1}\) and \(I_{2}\) as shown in the adjacent figure. If ratio of their radii is \(1: 2\) and ratio of the flux densities at \(O\) due to \(A\) and \(B\) is \(1: 3\) then the value of \(I_{1} /\) \(I_{2}\) is


