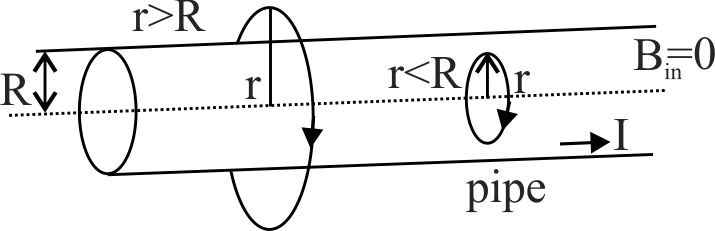
362616
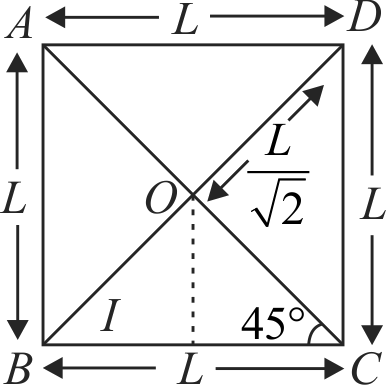
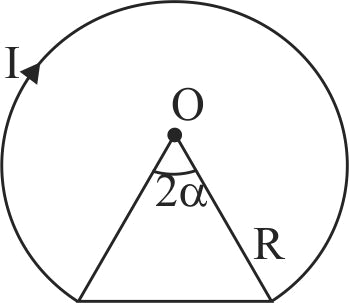
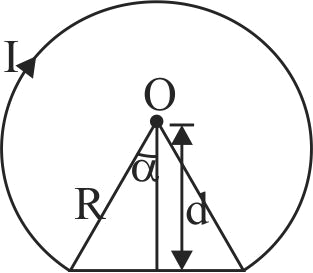
Two thick wires and two thin wires, all of same material and same length, form a square in three different ways \(P,Q\) and \(R\) as shown in the figure. With correct connections shown, the magnetic field due to the current flow, at the centre of the loop will be zero in case of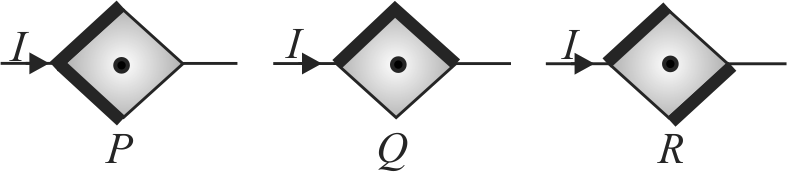
362616
Two thick wires and two thin wires, all of same material and same length, form a square in three different ways \(P,Q\) and \(R\) as shown in the figure. With correct connections shown, the magnetic field due to the current flow, at the centre of the loop will be zero in case of
362616
Two thick wires and two thin wires, all of same material and same length, form a square in three different ways \(P,Q\) and \(R\) as shown in the figure. With correct connections shown, the magnetic field due to the current flow, at the centre of the loop will be zero in case of
362616
Two thick wires and two thin wires, all of same material and same length, form a square in three different ways \(P,Q\) and \(R\) as shown in the figure. With correct connections shown, the magnetic field due to the current flow, at the centre of the loop will be zero in case of