362617 The magnetic field at the point of intersection of diagonals of a square loop of side \(L\) carrying a current \(I\) is found to be \(N \dfrac{\mu_{0} I}{\pi L}\). find the value of \(N\).

362618 Figure shows a straight wire of length \(l\) carrying current \(i\). The magnitude of magnetic field produced by the current at point \(P\) is

362619 A particle is moving with velocity \(\vec v = \widehat i + 3\widehat j\) and it produces an electric field at a point given by \(\vec E = 2\widehat k\). It will produce magnetic field at that point equal to (all quantities are in SI units)

362620 An elevator carrying a charge of 0.5 \(C\) is moving down with a velocity of \({5 \times 10^{3} {~m} {~s}^{-1}}\). The elevator is 4 \(m\) from the bottom and 3 \(m\) horizontally from \({P}\) as shown in figure. What magnetic field (in \({\mu {T})}\) does it produce at point \({P}\)?

362617 The magnetic field at the point of intersection of diagonals of a square loop of side \(L\) carrying a current \(I\) is found to be \(N \dfrac{\mu_{0} I}{\pi L}\). find the value of \(N\).

362618 Figure shows a straight wire of length \(l\) carrying current \(i\). The magnitude of magnetic field produced by the current at point \(P\) is

362619 A particle is moving with velocity \(\vec v = \widehat i + 3\widehat j\) and it produces an electric field at a point given by \(\vec E = 2\widehat k\). It will produce magnetic field at that point equal to (all quantities are in SI units)

362620 An elevator carrying a charge of 0.5 \(C\) is moving down with a velocity of \({5 \times 10^{3} {~m} {~s}^{-1}}\). The elevator is 4 \(m\) from the bottom and 3 \(m\) horizontally from \({P}\) as shown in figure. What magnetic field (in \({\mu {T})}\) does it produce at point \({P}\)?

362617 The magnetic field at the point of intersection of diagonals of a square loop of side \(L\) carrying a current \(I\) is found to be \(N \dfrac{\mu_{0} I}{\pi L}\). find the value of \(N\).

362618 Figure shows a straight wire of length \(l\) carrying current \(i\). The magnitude of magnetic field produced by the current at point \(P\) is

362619 A particle is moving with velocity \(\vec v = \widehat i + 3\widehat j\) and it produces an electric field at a point given by \(\vec E = 2\widehat k\). It will produce magnetic field at that point equal to (all quantities are in SI units)

362620 An elevator carrying a charge of 0.5 \(C\) is moving down with a velocity of \({5 \times 10^{3} {~m} {~s}^{-1}}\). The elevator is 4 \(m\) from the bottom and 3 \(m\) horizontally from \({P}\) as shown in figure. What magnetic field (in \({\mu {T})}\) does it produce at point \({P}\)?

362617 The magnetic field at the point of intersection of diagonals of a square loop of side \(L\) carrying a current \(I\) is found to be \(N \dfrac{\mu_{0} I}{\pi L}\). find the value of \(N\).

362618 Figure shows a straight wire of length \(l\) carrying current \(i\). The magnitude of magnetic field produced by the current at point \(P\) is

362619 A particle is moving with velocity \(\vec v = \widehat i + 3\widehat j\) and it produces an electric field at a point given by \(\vec E = 2\widehat k\). It will produce magnetic field at that point equal to (all quantities are in SI units)

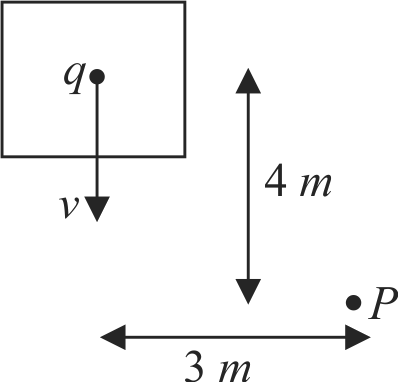
362620 An elevator carrying a charge of 0.5 \(C\) is moving down with a velocity of \({5 \times 10^{3} {~m} {~s}^{-1}}\). The elevator is 4 \(m\) from the bottom and 3 \(m\) horizontally from \({P}\) as shown in figure. What magnetic field (in \({\mu {T})}\) does it produce at point \({P}\)?