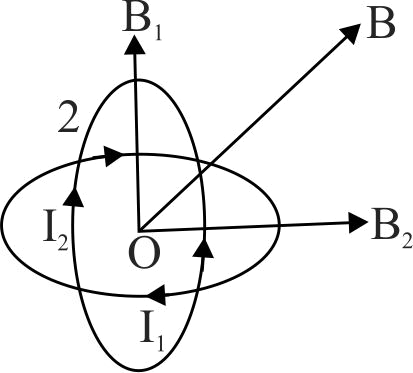
362574 Two concentric coils each of radius equal to \(2 \pi\) \(cm\) are placed right angles to each other. If 3\(A\) and 4\(A\) are the currents flowing through the two coils respectively. The magnetic induction (in \(Wb{m^{ - 2}}\) ) at the centre of the coils will be

362575 A tightly wound 100 turns coil of radius \(10\,cm\) carries a current of \(7\,A\). The magnitude of the magnetic field at the centre of the coil is (Take permeability of free space as \({4 \pi \times 10^{-7} S I}\) units):

362576 Assertion :
The magnetic field intensity at the centre of a circular coil carrying current changes, if the current through the coil is doubled.
Reason :
The magnetic field intensity does not depend on radius of coil.

362577 Shown in the figure is a conductor carrying a current ' \({I}\) '.

The magnetic field intensity at the common centre of all the three arcs (point \(O\)) is

362578 A circular coil carrying a certain current produces a magnetic field \({B_0}\) at its centre. The coil is now rewound so as to have 3 turns and the same curent is passed through it. The new magnetic field at the centre is

362574 Two concentric coils each of radius equal to \(2 \pi\) \(cm\) are placed right angles to each other. If 3\(A\) and 4\(A\) are the currents flowing through the two coils respectively. The magnetic induction (in \(Wb{m^{ - 2}}\) ) at the centre of the coils will be

362575 A tightly wound 100 turns coil of radius \(10\,cm\) carries a current of \(7\,A\). The magnitude of the magnetic field at the centre of the coil is (Take permeability of free space as \({4 \pi \times 10^{-7} S I}\) units):

362576 Assertion :
The magnetic field intensity at the centre of a circular coil carrying current changes, if the current through the coil is doubled.
Reason :
The magnetic field intensity does not depend on radius of coil.

362577 Shown in the figure is a conductor carrying a current ' \({I}\) '.

The magnetic field intensity at the common centre of all the three arcs (point \(O\)) is

362578 A circular coil carrying a certain current produces a magnetic field \({B_0}\) at its centre. The coil is now rewound so as to have 3 turns and the same curent is passed through it. The new magnetic field at the centre is

362574 Two concentric coils each of radius equal to \(2 \pi\) \(cm\) are placed right angles to each other. If 3\(A\) and 4\(A\) are the currents flowing through the two coils respectively. The magnetic induction (in \(Wb{m^{ - 2}}\) ) at the centre of the coils will be

362575 A tightly wound 100 turns coil of radius \(10\,cm\) carries a current of \(7\,A\). The magnitude of the magnetic field at the centre of the coil is (Take permeability of free space as \({4 \pi \times 10^{-7} S I}\) units):

362576 Assertion :
The magnetic field intensity at the centre of a circular coil carrying current changes, if the current through the coil is doubled.
Reason :
The magnetic field intensity does not depend on radius of coil.

362577 Shown in the figure is a conductor carrying a current ' \({I}\) '.

The magnetic field intensity at the common centre of all the three arcs (point \(O\)) is

362578 A circular coil carrying a certain current produces a magnetic field \({B_0}\) at its centre. The coil is now rewound so as to have 3 turns and the same curent is passed through it. The new magnetic field at the centre is

362574 Two concentric coils each of radius equal to \(2 \pi\) \(cm\) are placed right angles to each other. If 3\(A\) and 4\(A\) are the currents flowing through the two coils respectively. The magnetic induction (in \(Wb{m^{ - 2}}\) ) at the centre of the coils will be

362575 A tightly wound 100 turns coil of radius \(10\,cm\) carries a current of \(7\,A\). The magnitude of the magnetic field at the centre of the coil is (Take permeability of free space as \({4 \pi \times 10^{-7} S I}\) units):

362576 Assertion :
The magnetic field intensity at the centre of a circular coil carrying current changes, if the current through the coil is doubled.
Reason :
The magnetic field intensity does not depend on radius of coil.

362577 Shown in the figure is a conductor carrying a current ' \({I}\) '.

The magnetic field intensity at the common centre of all the three arcs (point \(O\)) is

362578 A circular coil carrying a certain current produces a magnetic field \({B_0}\) at its centre. The coil is now rewound so as to have 3 turns and the same curent is passed through it. The new magnetic field at the centre is

362574 Two concentric coils each of radius equal to \(2 \pi\) \(cm\) are placed right angles to each other. If 3\(A\) and 4\(A\) are the currents flowing through the two coils respectively. The magnetic induction (in \(Wb{m^{ - 2}}\) ) at the centre of the coils will be

362575 A tightly wound 100 turns coil of radius \(10\,cm\) carries a current of \(7\,A\). The magnitude of the magnetic field at the centre of the coil is (Take permeability of free space as \({4 \pi \times 10^{-7} S I}\) units):

362576 Assertion :
The magnetic field intensity at the centre of a circular coil carrying current changes, if the current through the coil is doubled.
Reason :
The magnetic field intensity does not depend on radius of coil.

362577 Shown in the figure is a conductor carrying a current ' \({I}\) '.

The magnetic field intensity at the common centre of all the three arcs (point \(O\)) is

362578 A circular coil carrying a certain current produces a magnetic field \({B_0}\) at its centre. The coil is now rewound so as to have 3 turns and the same curent is passed through it. The new magnetic field at the centre is