Explanation:
Suppose the two bodies \(A\) and \(B\) meet at
time \(t\), at a height \(\dfrac{H}{2}\) from the ground
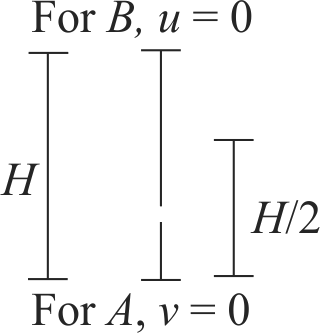
For body \(B,u = 0\),
\(h = \frac{H}{2}\)
\( \Rightarrow \quad h = ut + \frac{1}{2}g{t^2}\)
Hence \(\quad \frac{H}{2} = \frac{1}{2}g{t^2}\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
For body \(A,\quad u = {v_0},h = \frac{H}{2}\)
\( \Rightarrow \quad h = ut - \frac{1}{2}g{t^2}\)
Hence, \(\frac{H}{2} = {v_0}t - \frac{1}{2}g{t^2}\,\,\,\,\,\,\,\,\,\,\,(2)\)
So,from Eq.(1) and (2) we get,
\({v_0}t - \frac{1}{2}g{t^2} = \frac{1}{2}g{t^2} \Rightarrow {v_0}t = g{t^2}\)
\( \Rightarrow t = \frac{{{v_0}}}{g}\)
Now putting this value in Eq. (1), we get
\(\frac{H}{2} = \frac{1}{2}g \times \frac{{v_0^2}}{{{g^2}}}\)
\( \Rightarrow H = \frac{{v_0^2}}{g}\)
\( \Rightarrow {v_0} = \sqrt {gH} \)