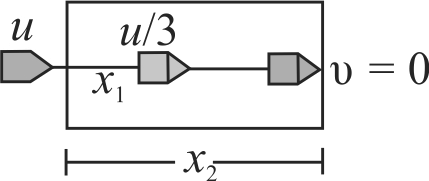
362323 A bullet from a gun is fired on a rectangular wooden block with velocity \(u\). When bullet travels \(24\,cm\) through the block along its length horizontally, velocity of bullet becomes \(\frac{u}{3}\). Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is:
362323 A bullet from a gun is fired on a rectangular wooden block with velocity \(u\). When bullet travels \(24\,cm\) through the block along its length horizontally, velocity of bullet becomes \(\frac{u}{3}\). Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is:
362323 A bullet from a gun is fired on a rectangular wooden block with velocity \(u\). When bullet travels \(24\,cm\) through the block along its length horizontally, velocity of bullet becomes \(\frac{u}{3}\). Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is:
362323 A bullet from a gun is fired on a rectangular wooden block with velocity \(u\). When bullet travels \(24\,cm\) through the block along its length horizontally, velocity of bullet becomes \(\frac{u}{3}\). Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is:
362323 A bullet from a gun is fired on a rectangular wooden block with velocity \(u\). When bullet travels \(24\,cm\) through the block along its length horizontally, velocity of bullet becomes \(\frac{u}{3}\). Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is: