361813
A small car \(A\) starts moving on a horizontal surface, assumed to be \(X-Y\) plane along a straight line parallel to \(X\)-axis (see figure) with a constant acceleration of \(4 {~m} / {s}^{2}\). Initially it is located on the positive \(Y\)-axis at a distance 9 \(m\) from origin. At the instant the car starts moving, a ball is rolled along the surface from the origin in a direction making an angle \(45^{\circ}\) with the \(X\)-axis. The ball moves without friction at a constant velocity and hits the car. Find the speed of the ball.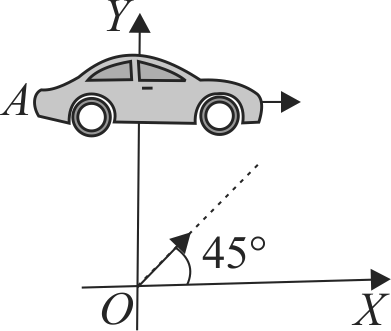
361815
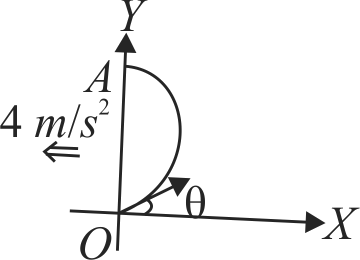
In the given figure, particle \(A\) moves along the line \(y=30\) \(m\) with a constant velocity \(\vec{v}\) of magnitude \(3.0 {~m} / {s}\) and parallel to the \(x\)-axis. At the instant particle \(A\) passes the \(y\)-axis, particle \(B\) leaves the origin with a zero initial speed and a constant acceleration \(\vec{a}\) of magnitude \(0.40 {~m} / {s}^{2}\). What angle \(\theta\) between \(\vec{a}\) and the positive direction of the \(y\)-axis would result in a collision?
361813
A small car \(A\) starts moving on a horizontal surface, assumed to be \(X-Y\) plane along a straight line parallel to \(X\)-axis (see figure) with a constant acceleration of \(4 {~m} / {s}^{2}\). Initially it is located on the positive \(Y\)-axis at a distance 9 \(m\) from origin. At the instant the car starts moving, a ball is rolled along the surface from the origin in a direction making an angle \(45^{\circ}\) with the \(X\)-axis. The ball moves without friction at a constant velocity and hits the car. Find the speed of the ball.
361815
In the given figure, particle \(A\) moves along the line \(y=30\) \(m\) with a constant velocity \(\vec{v}\) of magnitude \(3.0 {~m} / {s}\) and parallel to the \(x\)-axis. At the instant particle \(A\) passes the \(y\)-axis, particle \(B\) leaves the origin with a zero initial speed and a constant acceleration \(\vec{a}\) of magnitude \(0.40 {~m} / {s}^{2}\). What angle \(\theta\) between \(\vec{a}\) and the positive direction of the \(y\)-axis would result in a collision?
361813
A small car \(A\) starts moving on a horizontal surface, assumed to be \(X-Y\) plane along a straight line parallel to \(X\)-axis (see figure) with a constant acceleration of \(4 {~m} / {s}^{2}\). Initially it is located on the positive \(Y\)-axis at a distance 9 \(m\) from origin. At the instant the car starts moving, a ball is rolled along the surface from the origin in a direction making an angle \(45^{\circ}\) with the \(X\)-axis. The ball moves without friction at a constant velocity and hits the car. Find the speed of the ball.
361815
In the given figure, particle \(A\) moves along the line \(y=30\) \(m\) with a constant velocity \(\vec{v}\) of magnitude \(3.0 {~m} / {s}\) and parallel to the \(x\)-axis. At the instant particle \(A\) passes the \(y\)-axis, particle \(B\) leaves the origin with a zero initial speed and a constant acceleration \(\vec{a}\) of magnitude \(0.40 {~m} / {s}^{2}\). What angle \(\theta\) between \(\vec{a}\) and the positive direction of the \(y\)-axis would result in a collision?
361813
A small car \(A\) starts moving on a horizontal surface, assumed to be \(X-Y\) plane along a straight line parallel to \(X\)-axis (see figure) with a constant acceleration of \(4 {~m} / {s}^{2}\). Initially it is located on the positive \(Y\)-axis at a distance 9 \(m\) from origin. At the instant the car starts moving, a ball is rolled along the surface from the origin in a direction making an angle \(45^{\circ}\) with the \(X\)-axis. The ball moves without friction at a constant velocity and hits the car. Find the speed of the ball.
361815
In the given figure, particle \(A\) moves along the line \(y=30\) \(m\) with a constant velocity \(\vec{v}\) of magnitude \(3.0 {~m} / {s}\) and parallel to the \(x\)-axis. At the instant particle \(A\) passes the \(y\)-axis, particle \(B\) leaves the origin with a zero initial speed and a constant acceleration \(\vec{a}\) of magnitude \(0.40 {~m} / {s}^{2}\). What angle \(\theta\) between \(\vec{a}\) and the positive direction of the \(y\)-axis would result in a collision?
361813
A small car \(A\) starts moving on a horizontal surface, assumed to be \(X-Y\) plane along a straight line parallel to \(X\)-axis (see figure) with a constant acceleration of \(4 {~m} / {s}^{2}\). Initially it is located on the positive \(Y\)-axis at a distance 9 \(m\) from origin. At the instant the car starts moving, a ball is rolled along the surface from the origin in a direction making an angle \(45^{\circ}\) with the \(X\)-axis. The ball moves without friction at a constant velocity and hits the car. Find the speed of the ball.
361815
In the given figure, particle \(A\) moves along the line \(y=30\) \(m\) with a constant velocity \(\vec{v}\) of magnitude \(3.0 {~m} / {s}\) and parallel to the \(x\)-axis. At the instant particle \(A\) passes the \(y\)-axis, particle \(B\) leaves the origin with a zero initial speed and a constant acceleration \(\vec{a}\) of magnitude \(0.40 {~m} / {s}^{2}\). What angle \(\theta\) between \(\vec{a}\) and the positive direction of the \(y\)-axis would result in a collision?