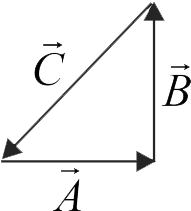
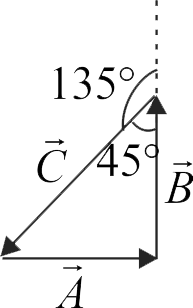
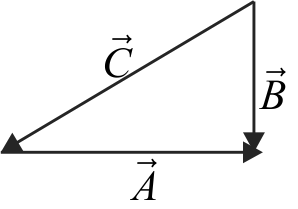
361768 The vectors \(\overrightarrow A ,\overrightarrow B \) and \(\overrightarrow C \) are such that \(|\overrightarrow A | = |\vec B|,|\vec C| = \sqrt 2 |\overrightarrow A |\) and \(\overrightarrow A + \vec B + \vec C = 0.\) The angle (in degrees) between \(\vec{B}\) and \(\vec{C}\) is
361768 The vectors \(\overrightarrow A ,\overrightarrow B \) and \(\overrightarrow C \) are such that \(|\overrightarrow A | = |\vec B|,|\vec C| = \sqrt 2 |\overrightarrow A |\) and \(\overrightarrow A + \vec B + \vec C = 0.\) The angle (in degrees) between \(\vec{B}\) and \(\vec{C}\) is
361768 The vectors \(\overrightarrow A ,\overrightarrow B \) and \(\overrightarrow C \) are such that \(|\overrightarrow A | = |\vec B|,|\vec C| = \sqrt 2 |\overrightarrow A |\) and \(\overrightarrow A + \vec B + \vec C = 0.\) The angle (in degrees) between \(\vec{B}\) and \(\vec{C}\) is
361768 The vectors \(\overrightarrow A ,\overrightarrow B \) and \(\overrightarrow C \) are such that \(|\overrightarrow A | = |\vec B|,|\vec C| = \sqrt 2 |\overrightarrow A |\) and \(\overrightarrow A + \vec B + \vec C = 0.\) The angle (in degrees) between \(\vec{B}\) and \(\vec{C}\) is