369902
Two wires of the same meaterial (Young's modulus = Y) and same length \({\text{ }}L\) but radii \(R\) and \(2R\) respectively are joined end to end and a weight w is suspended from the combination as shown in figure. The elastic potential energy in the system is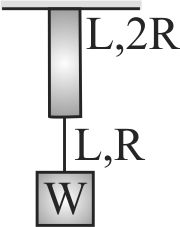
369905 A wire of initial length \(L\) and radius \(r\) is stretched by a length \(x\). Another wire of same material but with initial length \(2L\,{\text{and}}\,2r\) is stretched by a length \(2x\). The ratio of the stored elastic energy per unit volume in the first and second wire is
369902
Two wires of the same meaterial (Young's modulus = Y) and same length \({\text{ }}L\) but radii \(R\) and \(2R\) respectively are joined end to end and a weight w is suspended from the combination as shown in figure. The elastic potential energy in the system is
369905 A wire of initial length \(L\) and radius \(r\) is stretched by a length \(x\). Another wire of same material but with initial length \(2L\,{\text{and}}\,2r\) is stretched by a length \(2x\). The ratio of the stored elastic energy per unit volume in the first and second wire is
369902
Two wires of the same meaterial (Young's modulus = Y) and same length \({\text{ }}L\) but radii \(R\) and \(2R\) respectively are joined end to end and a weight w is suspended from the combination as shown in figure. The elastic potential energy in the system is
369905 A wire of initial length \(L\) and radius \(r\) is stretched by a length \(x\). Another wire of same material but with initial length \(2L\,{\text{and}}\,2r\) is stretched by a length \(2x\). The ratio of the stored elastic energy per unit volume in the first and second wire is
369902
Two wires of the same meaterial (Young's modulus = Y) and same length \({\text{ }}L\) but radii \(R\) and \(2R\) respectively are joined end to end and a weight w is suspended from the combination as shown in figure. The elastic potential energy in the system is
369905 A wire of initial length \(L\) and radius \(r\) is stretched by a length \(x\). Another wire of same material but with initial length \(2L\,{\text{and}}\,2r\) is stretched by a length \(2x\). The ratio of the stored elastic energy per unit volume in the first and second wire is
369902
Two wires of the same meaterial (Young's modulus = Y) and same length \({\text{ }}L\) but radii \(R\) and \(2R\) respectively are joined end to end and a weight w is suspended from the combination as shown in figure. The elastic potential energy in the system is
369905 A wire of initial length \(L\) and radius \(r\) is stretched by a length \(x\). Another wire of same material but with initial length \(2L\,{\text{and}}\,2r\) is stretched by a length \(2x\). The ratio of the stored elastic energy per unit volume in the first and second wire is