369879 Young's moduli of the material of wires \(A\) and \(B\) are in the ratio of \(1: 4\), while its area of cross sections are in the ratio of \(1: 3\). If the same amount of load is applied to both the wires, the amount of elongation produced in the wires \(A\) and \(B\) will be in the ratio of [Assume length of wires \(A\) and \(B\) are same]
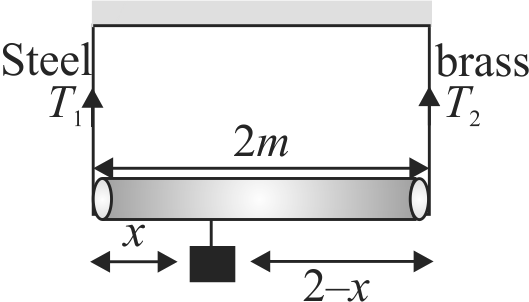
369880 A light rod of length \(2\;m\) is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its end. One of the wires is made of steel of cross-section \(0.1\;c{m^2}\). The other wire is of brass of cross-section \(0.2\;c{m^2}\). A weight is suspended from a certain point of the rod such that equal stresses are produced in both the wires. The rod remians horizontal in this case also. Find out the position of the load from the steel wire.
369879 Young's moduli of the material of wires \(A\) and \(B\) are in the ratio of \(1: 4\), while its area of cross sections are in the ratio of \(1: 3\). If the same amount of load is applied to both the wires, the amount of elongation produced in the wires \(A\) and \(B\) will be in the ratio of [Assume length of wires \(A\) and \(B\) are same]
369880 A light rod of length \(2\;m\) is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its end. One of the wires is made of steel of cross-section \(0.1\;c{m^2}\). The other wire is of brass of cross-section \(0.2\;c{m^2}\). A weight is suspended from a certain point of the rod such that equal stresses are produced in both the wires. The rod remians horizontal in this case also. Find out the position of the load from the steel wire.
369879 Young's moduli of the material of wires \(A\) and \(B\) are in the ratio of \(1: 4\), while its area of cross sections are in the ratio of \(1: 3\). If the same amount of load is applied to both the wires, the amount of elongation produced in the wires \(A\) and \(B\) will be in the ratio of [Assume length of wires \(A\) and \(B\) are same]
369880 A light rod of length \(2\;m\) is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its end. One of the wires is made of steel of cross-section \(0.1\;c{m^2}\). The other wire is of brass of cross-section \(0.2\;c{m^2}\). A weight is suspended from a certain point of the rod such that equal stresses are produced in both the wires. The rod remians horizontal in this case also. Find out the position of the load from the steel wire.
369879 Young's moduli of the material of wires \(A\) and \(B\) are in the ratio of \(1: 4\), while its area of cross sections are in the ratio of \(1: 3\). If the same amount of load is applied to both the wires, the amount of elongation produced in the wires \(A\) and \(B\) will be in the ratio of [Assume length of wires \(A\) and \(B\) are same]
369880 A light rod of length \(2\;m\) is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its end. One of the wires is made of steel of cross-section \(0.1\;c{m^2}\). The other wire is of brass of cross-section \(0.2\;c{m^2}\). A weight is suspended from a certain point of the rod such that equal stresses are produced in both the wires. The rod remians horizontal in this case also. Find out the position of the load from the steel wire.
369879 Young's moduli of the material of wires \(A\) and \(B\) are in the ratio of \(1: 4\), while its area of cross sections are in the ratio of \(1: 3\). If the same amount of load is applied to both the wires, the amount of elongation produced in the wires \(A\) and \(B\) will be in the ratio of [Assume length of wires \(A\) and \(B\) are same]
369880 A light rod of length \(2\;m\) is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its end. One of the wires is made of steel of cross-section \(0.1\;c{m^2}\). The other wire is of brass of cross-section \(0.2\;c{m^2}\). A weight is suspended from a certain point of the rod such that equal stresses are produced in both the wires. The rod remians horizontal in this case also. Find out the position of the load from the steel wire.