369857 An iron wire and copper wire having same length and cross-section are suspended from same roof Young's modulus of copper is \(1 / 3 \mathrm{rd}\) that of iron. Then the ratio of the weights to be added at their ends so that their ends are at the same level is
369858
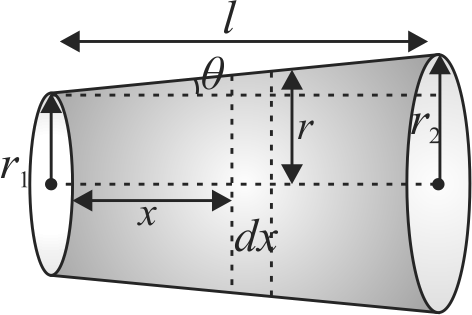
A slightly conical wire of length \(l\) and radii \(r_{1}\) and \(r_{2}\) is stretched by two forces each of magnitude \(F\) applied parallel to length in opposite directions and normal to end faces. If \(Y\) denotes the Young's modulus, then find the elongation of the wire \(\left(r_{1}>r_{2}\right)\).
369860
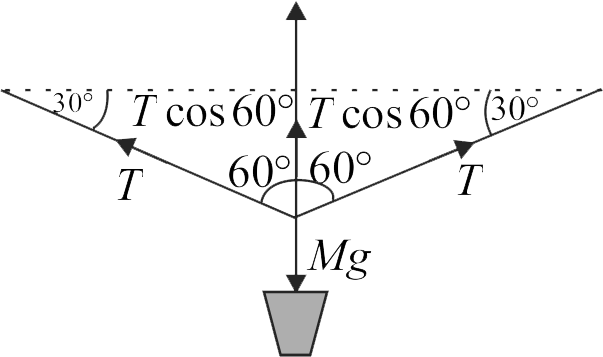
A \(45 - kg\) traffic light is suspended with two steel wires of equal lengths and radii of \(0.5\;cm\). If the wires make an angle of \(30^{\circ}\) with the horizontal, the fractional increase in their length due to the weight of the traffic light is \(C \times {10^{ - 5}}.\) Find \(C\). (Young's modulus of steel \( = 2 \times {10^{11}}N{m^{ - 2}}.\)
\(\pi=3.14\) and \(g = 9.8\;m{\rm{/}}{s^2}\))
369857 An iron wire and copper wire having same length and cross-section are suspended from same roof Young's modulus of copper is \(1 / 3 \mathrm{rd}\) that of iron. Then the ratio of the weights to be added at their ends so that their ends are at the same level is
369858
A slightly conical wire of length \(l\) and radii \(r_{1}\) and \(r_{2}\) is stretched by two forces each of magnitude \(F\) applied parallel to length in opposite directions and normal to end faces. If \(Y\) denotes the Young's modulus, then find the elongation of the wire \(\left(r_{1}>r_{2}\right)\).
369860
A \(45 - kg\) traffic light is suspended with two steel wires of equal lengths and radii of \(0.5\;cm\). If the wires make an angle of \(30^{\circ}\) with the horizontal, the fractional increase in their length due to the weight of the traffic light is \(C \times {10^{ - 5}}.\) Find \(C\). (Young's modulus of steel \( = 2 \times {10^{11}}N{m^{ - 2}}.\)
\(\pi=3.14\) and \(g = 9.8\;m{\rm{/}}{s^2}\))
369857 An iron wire and copper wire having same length and cross-section are suspended from same roof Young's modulus of copper is \(1 / 3 \mathrm{rd}\) that of iron. Then the ratio of the weights to be added at their ends so that their ends are at the same level is
369858
A slightly conical wire of length \(l\) and radii \(r_{1}\) and \(r_{2}\) is stretched by two forces each of magnitude \(F\) applied parallel to length in opposite directions and normal to end faces. If \(Y\) denotes the Young's modulus, then find the elongation of the wire \(\left(r_{1}>r_{2}\right)\).
369860
A \(45 - kg\) traffic light is suspended with two steel wires of equal lengths and radii of \(0.5\;cm\). If the wires make an angle of \(30^{\circ}\) with the horizontal, the fractional increase in their length due to the weight of the traffic light is \(C \times {10^{ - 5}}.\) Find \(C\). (Young's modulus of steel \( = 2 \times {10^{11}}N{m^{ - 2}}.\)
\(\pi=3.14\) and \(g = 9.8\;m{\rm{/}}{s^2}\))
369857 An iron wire and copper wire having same length and cross-section are suspended from same roof Young's modulus of copper is \(1 / 3 \mathrm{rd}\) that of iron. Then the ratio of the weights to be added at their ends so that their ends are at the same level is
369858
A slightly conical wire of length \(l\) and radii \(r_{1}\) and \(r_{2}\) is stretched by two forces each of magnitude \(F\) applied parallel to length in opposite directions and normal to end faces. If \(Y\) denotes the Young's modulus, then find the elongation of the wire \(\left(r_{1}>r_{2}\right)\).
369860
A \(45 - kg\) traffic light is suspended with two steel wires of equal lengths and radii of \(0.5\;cm\). If the wires make an angle of \(30^{\circ}\) with the horizontal, the fractional increase in their length due to the weight of the traffic light is \(C \times {10^{ - 5}}.\) Find \(C\). (Young's modulus of steel \( = 2 \times {10^{11}}N{m^{ - 2}}.\)
\(\pi=3.14\) and \(g = 9.8\;m{\rm{/}}{s^2}\))