369835
The adjacent graph shows the extension \((\Delta l)\) of a wire length \(1 \mathrm{~m}\) suspended from the top of a roof at one end with a load \(W\) connected to the other end. If the cross-sectional area of the wire is \(10^{-6} \mathrm{~m}^{2}\), calculate the Young's modulus of the material of the wire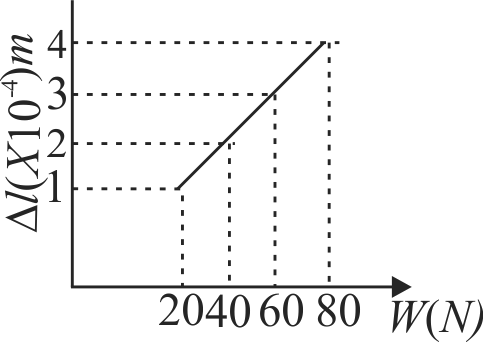
369839 Two rods of same material and volume having circular cross - section are subjected to tension \(T\). Within the elastic limit, same force is applied to both the rods. Diameter of the first rod is half of the second rod, then the extensions of first rod to second rod will be in the ratio
369835
The adjacent graph shows the extension \((\Delta l)\) of a wire length \(1 \mathrm{~m}\) suspended from the top of a roof at one end with a load \(W\) connected to the other end. If the cross-sectional area of the wire is \(10^{-6} \mathrm{~m}^{2}\), calculate the Young's modulus of the material of the wire
369839 Two rods of same material and volume having circular cross - section are subjected to tension \(T\). Within the elastic limit, same force is applied to both the rods. Diameter of the first rod is half of the second rod, then the extensions of first rod to second rod will be in the ratio
369835
The adjacent graph shows the extension \((\Delta l)\) of a wire length \(1 \mathrm{~m}\) suspended from the top of a roof at one end with a load \(W\) connected to the other end. If the cross-sectional area of the wire is \(10^{-6} \mathrm{~m}^{2}\), calculate the Young's modulus of the material of the wire
369839 Two rods of same material and volume having circular cross - section are subjected to tension \(T\). Within the elastic limit, same force is applied to both the rods. Diameter of the first rod is half of the second rod, then the extensions of first rod to second rod will be in the ratio
369835
The adjacent graph shows the extension \((\Delta l)\) of a wire length \(1 \mathrm{~m}\) suspended from the top of a roof at one end with a load \(W\) connected to the other end. If the cross-sectional area of the wire is \(10^{-6} \mathrm{~m}^{2}\), calculate the Young's modulus of the material of the wire
369839 Two rods of same material and volume having circular cross - section are subjected to tension \(T\). Within the elastic limit, same force is applied to both the rods. Diameter of the first rod is half of the second rod, then the extensions of first rod to second rod will be in the ratio
369835
The adjacent graph shows the extension \((\Delta l)\) of a wire length \(1 \mathrm{~m}\) suspended from the top of a roof at one end with a load \(W\) connected to the other end. If the cross-sectional area of the wire is \(10^{-6} \mathrm{~m}^{2}\), calculate the Young's modulus of the material of the wire
369839 Two rods of same material and volume having circular cross - section are subjected to tension \(T\). Within the elastic limit, same force is applied to both the rods. Diameter of the first rod is half of the second rod, then the extensions of first rod to second rod will be in the ratio
