369764
Assertion :
A hollow shaft is found to be stronger than a solid shaft made of same size and material.
Reason :
The torque required to produce a given twist in hollow cylinder is greater than that required to twist a solid cylinder of same size and material.
369765
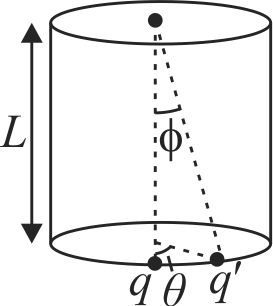
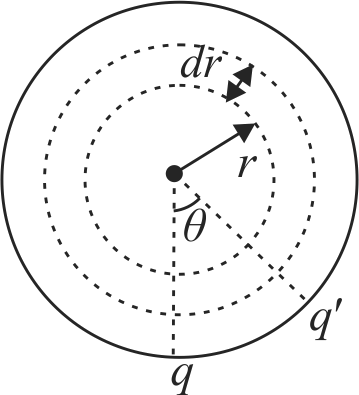
Consider a solid cylinder having length \(\mathrm{L}\) and radius \(a\). The upper end of the cylinder is fixed to the ceiling. The lower end of the cylinder is twisted by an angle \(\theta\) then find the restoring torque produced in the rod. Given that \(\eta\) is the shear modulus.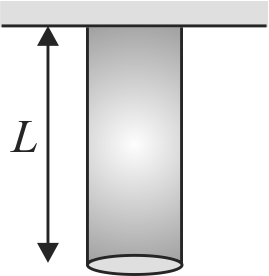
369766 The edge of an aluminium cube is \(10\;cm\) long. One face of the cube is firmly fixed to a vertical wall. A mass of \(100\;kg\) is then attached to the opposite face of the cube. The shear modulus of aluminium is \(25\,GPa\) Then the vertical deflection of this face
369764
Assertion :
A hollow shaft is found to be stronger than a solid shaft made of same size and material.
Reason :
The torque required to produce a given twist in hollow cylinder is greater than that required to twist a solid cylinder of same size and material.
369765
Consider a solid cylinder having length \(\mathrm{L}\) and radius \(a\). The upper end of the cylinder is fixed to the ceiling. The lower end of the cylinder is twisted by an angle \(\theta\) then find the restoring torque produced in the rod. Given that \(\eta\) is the shear modulus.
369766 The edge of an aluminium cube is \(10\;cm\) long. One face of the cube is firmly fixed to a vertical wall. A mass of \(100\;kg\) is then attached to the opposite face of the cube. The shear modulus of aluminium is \(25\,GPa\) Then the vertical deflection of this face
369764
Assertion :
A hollow shaft is found to be stronger than a solid shaft made of same size and material.
Reason :
The torque required to produce a given twist in hollow cylinder is greater than that required to twist a solid cylinder of same size and material.
369765
Consider a solid cylinder having length \(\mathrm{L}\) and radius \(a\). The upper end of the cylinder is fixed to the ceiling. The lower end of the cylinder is twisted by an angle \(\theta\) then find the restoring torque produced in the rod. Given that \(\eta\) is the shear modulus.
369766 The edge of an aluminium cube is \(10\;cm\) long. One face of the cube is firmly fixed to a vertical wall. A mass of \(100\;kg\) is then attached to the opposite face of the cube. The shear modulus of aluminium is \(25\,GPa\) Then the vertical deflection of this face
369764
Assertion :
A hollow shaft is found to be stronger than a solid shaft made of same size and material.
Reason :
The torque required to produce a given twist in hollow cylinder is greater than that required to twist a solid cylinder of same size and material.
369765
Consider a solid cylinder having length \(\mathrm{L}\) and radius \(a\). The upper end of the cylinder is fixed to the ceiling. The lower end of the cylinder is twisted by an angle \(\theta\) then find the restoring torque produced in the rod. Given that \(\eta\) is the shear modulus.
369766 The edge of an aluminium cube is \(10\;cm\) long. One face of the cube is firmly fixed to a vertical wall. A mass of \(100\;kg\) is then attached to the opposite face of the cube. The shear modulus of aluminium is \(25\,GPa\) Then the vertical deflection of this face