369668 A stress of \(6 \times {10^6}N{m^{ - 2}}\) required for breaking a material. The density \(\rho\) of the material is \(3 \times {10^3}\;kg\;{m^{ - 3}}.\) If the wire is to break under its own weight, the length of the wire made of that material should be (take, \(g = 10\;m{s^{ - 2}}\) )
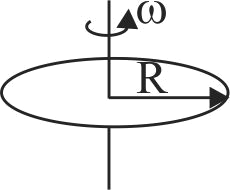
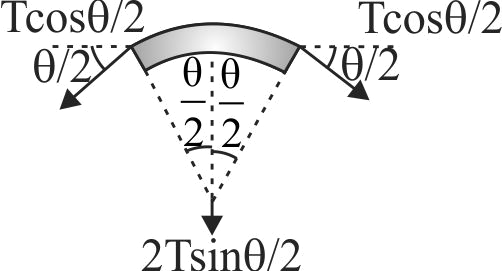
369669 A ring of radius \(\mathrm{R}\) made of lead wire breaking strength \(\sigma\) and density \(\rho\), roatated about stationary vertical axis passing through its centre and perpendicular to the plane of the ring. Calculate the number of rotations per second at which the ring ruptures
369668 A stress of \(6 \times {10^6}N{m^{ - 2}}\) required for breaking a material. The density \(\rho\) of the material is \(3 \times {10^3}\;kg\;{m^{ - 3}}.\) If the wire is to break under its own weight, the length of the wire made of that material should be (take, \(g = 10\;m{s^{ - 2}}\) )
369669 A ring of radius \(\mathrm{R}\) made of lead wire breaking strength \(\sigma\) and density \(\rho\), roatated about stationary vertical axis passing through its centre and perpendicular to the plane of the ring. Calculate the number of rotations per second at which the ring ruptures
369668 A stress of \(6 \times {10^6}N{m^{ - 2}}\) required for breaking a material. The density \(\rho\) of the material is \(3 \times {10^3}\;kg\;{m^{ - 3}}.\) If the wire is to break under its own weight, the length of the wire made of that material should be (take, \(g = 10\;m{s^{ - 2}}\) )
369669 A ring of radius \(\mathrm{R}\) made of lead wire breaking strength \(\sigma\) and density \(\rho\), roatated about stationary vertical axis passing through its centre and perpendicular to the plane of the ring. Calculate the number of rotations per second at which the ring ruptures
369668 A stress of \(6 \times {10^6}N{m^{ - 2}}\) required for breaking a material. The density \(\rho\) of the material is \(3 \times {10^3}\;kg\;{m^{ - 3}}.\) If the wire is to break under its own weight, the length of the wire made of that material should be (take, \(g = 10\;m{s^{ - 2}}\) )
369669 A ring of radius \(\mathrm{R}\) made of lead wire breaking strength \(\sigma\) and density \(\rho\), roatated about stationary vertical axis passing through its centre and perpendicular to the plane of the ring. Calculate the number of rotations per second at which the ring ruptures