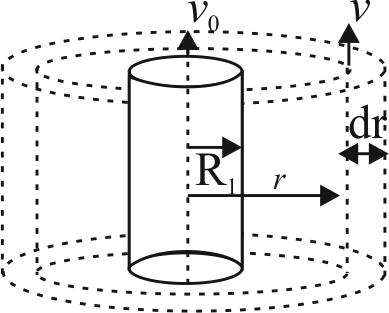
361334 A long cylinder of radius \(R_{1}\) is displaced along its axis with a constant velocity \(v_{0}\) inside a stationary co-axial cylinder of radius \(R_{2}\) as shown in the figure. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance \(r\) from the axis of the cylinders.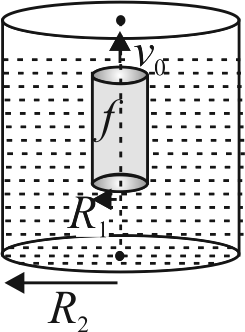

361335 Figure shows a long solid cylinder of radius \(R\) inside a long hollow tube of inner radius \(R^{\prime}\). A viscous liquid of coefficient of viscosity \(\eta\) is filled in the gap between the cylinder and the hollow tube. If the solid cylinder is moved with velocity \(v\) parallel to its length inside the fixed hollow tube, find the force required per unit length to be applied on the solid cylinder, assuming uniform velocity gradient in the liquid.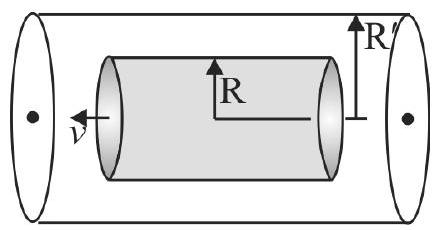

361336 A layer of glycerin of thinkness \(3\;mm\) is present between a large surface and a surface of area of \(0.2\;{m^2}\), with what force the small surface is to be pulled, so that it can move with a velocity of \(5\;m{\rm{/}}s\)? \(\left( {\eta = 0.09\,kg{m^{ - 1}}\;{s^{ - 1}}} \right)\).

361337 The velocity of water in a river is \(18\;km/hr\) near the surface. If the river is \(5\;m\) deep, find the shearing stress between the horizontal layers of water. The co-efficient of viscosity of water \(=10^{-2}\) poise.

361334 A long cylinder of radius \(R_{1}\) is displaced along its axis with a constant velocity \(v_{0}\) inside a stationary co-axial cylinder of radius \(R_{2}\) as shown in the figure. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance \(r\) from the axis of the cylinders.

361335 Figure shows a long solid cylinder of radius \(R\) inside a long hollow tube of inner radius \(R^{\prime}\). A viscous liquid of coefficient of viscosity \(\eta\) is filled in the gap between the cylinder and the hollow tube. If the solid cylinder is moved with velocity \(v\) parallel to its length inside the fixed hollow tube, find the force required per unit length to be applied on the solid cylinder, assuming uniform velocity gradient in the liquid.

361336 A layer of glycerin of thinkness \(3\;mm\) is present between a large surface and a surface of area of \(0.2\;{m^2}\), with what force the small surface is to be pulled, so that it can move with a velocity of \(5\;m{\rm{/}}s\)? \(\left( {\eta = 0.09\,kg{m^{ - 1}}\;{s^{ - 1}}} \right)\).

361337 The velocity of water in a river is \(18\;km/hr\) near the surface. If the river is \(5\;m\) deep, find the shearing stress between the horizontal layers of water. The co-efficient of viscosity of water \(=10^{-2}\) poise.

361334 A long cylinder of radius \(R_{1}\) is displaced along its axis with a constant velocity \(v_{0}\) inside a stationary co-axial cylinder of radius \(R_{2}\) as shown in the figure. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance \(r\) from the axis of the cylinders.

361335 Figure shows a long solid cylinder of radius \(R\) inside a long hollow tube of inner radius \(R^{\prime}\). A viscous liquid of coefficient of viscosity \(\eta\) is filled in the gap between the cylinder and the hollow tube. If the solid cylinder is moved with velocity \(v\) parallel to its length inside the fixed hollow tube, find the force required per unit length to be applied on the solid cylinder, assuming uniform velocity gradient in the liquid.

361336 A layer of glycerin of thinkness \(3\;mm\) is present between a large surface and a surface of area of \(0.2\;{m^2}\), with what force the small surface is to be pulled, so that it can move with a velocity of \(5\;m{\rm{/}}s\)? \(\left( {\eta = 0.09\,kg{m^{ - 1}}\;{s^{ - 1}}} \right)\).

361337 The velocity of water in a river is \(18\;km/hr\) near the surface. If the river is \(5\;m\) deep, find the shearing stress between the horizontal layers of water. The co-efficient of viscosity of water \(=10^{-2}\) poise.

361334 A long cylinder of radius \(R_{1}\) is displaced along its axis with a constant velocity \(v_{0}\) inside a stationary co-axial cylinder of radius \(R_{2}\) as shown in the figure. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance \(r\) from the axis of the cylinders.

361335 Figure shows a long solid cylinder of radius \(R\) inside a long hollow tube of inner radius \(R^{\prime}\). A viscous liquid of coefficient of viscosity \(\eta\) is filled in the gap between the cylinder and the hollow tube. If the solid cylinder is moved with velocity \(v\) parallel to its length inside the fixed hollow tube, find the force required per unit length to be applied on the solid cylinder, assuming uniform velocity gradient in the liquid.

361336 A layer of glycerin of thinkness \(3\;mm\) is present between a large surface and a surface of area of \(0.2\;{m^2}\), with what force the small surface is to be pulled, so that it can move with a velocity of \(5\;m{\rm{/}}s\)? \(\left( {\eta = 0.09\,kg{m^{ - 1}}\;{s^{ - 1}}} \right)\).

361337 The velocity of water in a river is \(18\;km/hr\) near the surface. If the river is \(5\;m\) deep, find the shearing stress between the horizontal layers of water. The co-efficient of viscosity of water \(=10^{-2}\) poise.