361319 A film of the liquid is supported in a vertical rectangular area. The top border of which is a sliding wire. An external force of \(5\,mN\) acts on the sliding wire of length \(50\;mm\) and linear mass density of \(1.75 \times {10^{ - 3}}\;kg/m\). Find the surface tension of the liquid.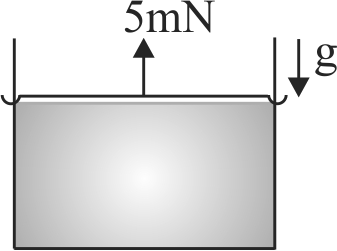

361320 A thin liquid film formed between a \(U\)-shaped wire and a light slider supports a weight of \(1.5 \times {10^{ - 2}}\;N\) (see figure). The length of the slider is \(30\;\,cm\) and its weight is negligible. The surface tension of the liquid film is

361321 There is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius \(R\). If the surface tension of the loop be \(T\), then what will be the tension in the thread?

361322 A rectangular frame of \(7\;cm \times 5\;cm\) hangs vertically by an arm of a balance. When its edge is just dipped in soap solution in container, extra mass of \(0.4\;g\) must be placed in opposite arm to balance the pull of the film in order to just raise it. Determine surface tension of soap solution in \({\rm{dyne/}}cm\).

361319 A film of the liquid is supported in a vertical rectangular area. The top border of which is a sliding wire. An external force of \(5\,mN\) acts on the sliding wire of length \(50\;mm\) and linear mass density of \(1.75 \times {10^{ - 3}}\;kg/m\). Find the surface tension of the liquid.

361320 A thin liquid film formed between a \(U\)-shaped wire and a light slider supports a weight of \(1.5 \times {10^{ - 2}}\;N\) (see figure). The length of the slider is \(30\;\,cm\) and its weight is negligible. The surface tension of the liquid film is

361321 There is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius \(R\). If the surface tension of the loop be \(T\), then what will be the tension in the thread?

361322 A rectangular frame of \(7\;cm \times 5\;cm\) hangs vertically by an arm of a balance. When its edge is just dipped in soap solution in container, extra mass of \(0.4\;g\) must be placed in opposite arm to balance the pull of the film in order to just raise it. Determine surface tension of soap solution in \({\rm{dyne/}}cm\).

361319 A film of the liquid is supported in a vertical rectangular area. The top border of which is a sliding wire. An external force of \(5\,mN\) acts on the sliding wire of length \(50\;mm\) and linear mass density of \(1.75 \times {10^{ - 3}}\;kg/m\). Find the surface tension of the liquid.

361320 A thin liquid film formed between a \(U\)-shaped wire and a light slider supports a weight of \(1.5 \times {10^{ - 2}}\;N\) (see figure). The length of the slider is \(30\;\,cm\) and its weight is negligible. The surface tension of the liquid film is

361321 There is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius \(R\). If the surface tension of the loop be \(T\), then what will be the tension in the thread?

361322 A rectangular frame of \(7\;cm \times 5\;cm\) hangs vertically by an arm of a balance. When its edge is just dipped in soap solution in container, extra mass of \(0.4\;g\) must be placed in opposite arm to balance the pull of the film in order to just raise it. Determine surface tension of soap solution in \({\rm{dyne/}}cm\).

361319 A film of the liquid is supported in a vertical rectangular area. The top border of which is a sliding wire. An external force of \(5\,mN\) acts on the sliding wire of length \(50\;mm\) and linear mass density of \(1.75 \times {10^{ - 3}}\;kg/m\). Find the surface tension of the liquid.

361320 A thin liquid film formed between a \(U\)-shaped wire and a light slider supports a weight of \(1.5 \times {10^{ - 2}}\;N\) (see figure). The length of the slider is \(30\;\,cm\) and its weight is negligible. The surface tension of the liquid film is

361321 There is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius \(R\). If the surface tension of the loop be \(T\), then what will be the tension in the thread?

361322 A rectangular frame of \(7\;cm \times 5\;cm\) hangs vertically by an arm of a balance. When its edge is just dipped in soap solution in container, extra mass of \(0.4\;g\) must be placed in opposite arm to balance the pull of the film in order to just raise it. Determine surface tension of soap solution in \({\rm{dyne/}}cm\).