361303
Bubbles are made by dipping a circular ring of radius \(b\) in a soap solution and then blowing air on the film formed on the ring. Assume that the blown air is in the form of a cylinder of radius \(b\). It has speed \(v\) and stops after striking the surface of the bubble being formed. The bubble grows spherically. Let the radius \(R\) of the bubble \((>>b)\), so that the air strikes the bubbles surface perpendicularly. The surface tension of the solution is \(T\) and air density is \(\rho\). The radius of the bubble when it separates from the ring is (neglect the mass of the bubble).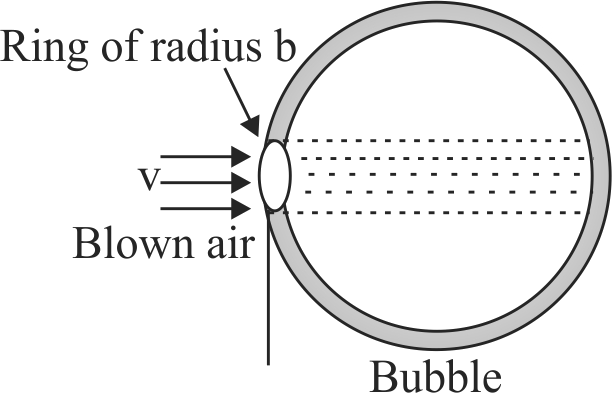
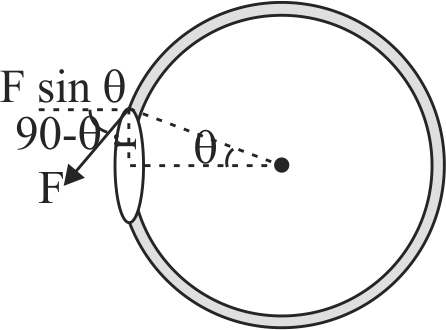
361304 A thin metal ring of internal radius \(8\;cm\) and external radius \(9\;cm\) is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. It is found that an extra weight of \(7.48\;g\) is required to pull the ring out of water. The surface tension of water is
361303
Bubbles are made by dipping a circular ring of radius \(b\) in a soap solution and then blowing air on the film formed on the ring. Assume that the blown air is in the form of a cylinder of radius \(b\). It has speed \(v\) and stops after striking the surface of the bubble being formed. The bubble grows spherically. Let the radius \(R\) of the bubble \((>>b)\), so that the air strikes the bubbles surface perpendicularly. The surface tension of the solution is \(T\) and air density is \(\rho\). The radius of the bubble when it separates from the ring is (neglect the mass of the bubble).
361304 A thin metal ring of internal radius \(8\;cm\) and external radius \(9\;cm\) is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. It is found that an extra weight of \(7.48\;g\) is required to pull the ring out of water. The surface tension of water is
361303
Bubbles are made by dipping a circular ring of radius \(b\) in a soap solution and then blowing air on the film formed on the ring. Assume that the blown air is in the form of a cylinder of radius \(b\). It has speed \(v\) and stops after striking the surface of the bubble being formed. The bubble grows spherically. Let the radius \(R\) of the bubble \((>>b)\), so that the air strikes the bubbles surface perpendicularly. The surface tension of the solution is \(T\) and air density is \(\rho\). The radius of the bubble when it separates from the ring is (neglect the mass of the bubble).
361304 A thin metal ring of internal radius \(8\;cm\) and external radius \(9\;cm\) is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. It is found that an extra weight of \(7.48\;g\) is required to pull the ring out of water. The surface tension of water is
361303
Bubbles are made by dipping a circular ring of radius \(b\) in a soap solution and then blowing air on the film formed on the ring. Assume that the blown air is in the form of a cylinder of radius \(b\). It has speed \(v\) and stops after striking the surface of the bubble being formed. The bubble grows spherically. Let the radius \(R\) of the bubble \((>>b)\), so that the air strikes the bubbles surface perpendicularly. The surface tension of the solution is \(T\) and air density is \(\rho\). The radius of the bubble when it separates from the ring is (neglect the mass of the bubble).
361304 A thin metal ring of internal radius \(8\;cm\) and external radius \(9\;cm\) is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. It is found that an extra weight of \(7.48\;g\) is required to pull the ring out of water. The surface tension of water is
361303
Bubbles are made by dipping a circular ring of radius \(b\) in a soap solution and then blowing air on the film formed on the ring. Assume that the blown air is in the form of a cylinder of radius \(b\). It has speed \(v\) and stops after striking the surface of the bubble being formed. The bubble grows spherically. Let the radius \(R\) of the bubble \((>>b)\), so that the air strikes the bubbles surface perpendicularly. The surface tension of the solution is \(T\) and air density is \(\rho\). The radius of the bubble when it separates from the ring is (neglect the mass of the bubble).
361304 A thin metal ring of internal radius \(8\;cm\) and external radius \(9\;cm\) is supported horizontally from the pan of a balance so that it comes in contact with water in a glass vessel. It is found that an extra weight of \(7.48\;g\) is required to pull the ring out of water. The surface tension of water is