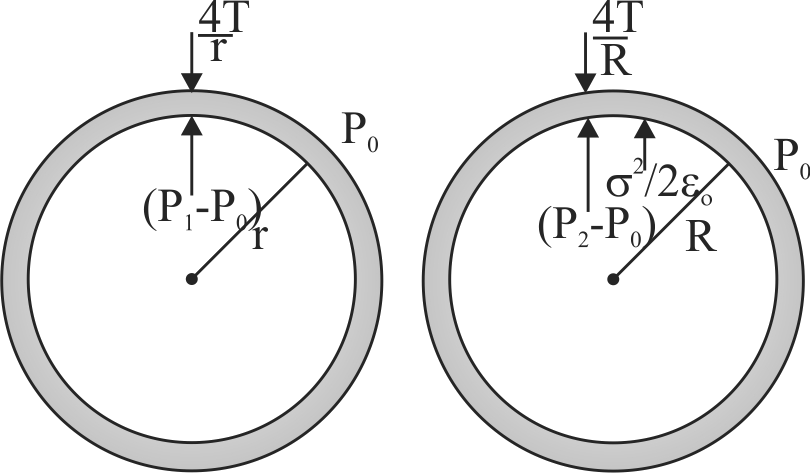361286 A soap bubble of radius ' \(r\) ' and surface tension ' \(T\) ' is given a charge. The new radius ' \(R\) ' of the bubble is related to its initial radius \(r\) by the equation, \(\left(P_{0}\right.\) is the atmospheric pressure & \(V\) is the final potential of the bubble
361286 A soap bubble of radius ' \(r\) ' and surface tension ' \(T\) ' is given a charge. The new radius ' \(R\) ' of the bubble is related to its initial radius \(r\) by the equation, \(\left(P_{0}\right.\) is the atmospheric pressure & \(V\) is the final potential of the bubble
361286 A soap bubble of radius ' \(r\) ' and surface tension ' \(T\) ' is given a charge. The new radius ' \(R\) ' of the bubble is related to its initial radius \(r\) by the equation, \(\left(P_{0}\right.\) is the atmospheric pressure & \(V\) is the final potential of the bubble
361286 A soap bubble of radius ' \(r\) ' and surface tension ' \(T\) ' is given a charge. The new radius ' \(R\) ' of the bubble is related to its initial radius \(r\) by the equation, \(\left(P_{0}\right.\) is the atmospheric pressure & \(V\) is the final potential of the bubble
361286 A soap bubble of radius ' \(r\) ' and surface tension ' \(T\) ' is given a charge. The new radius ' \(R\) ' of the bubble is related to its initial radius \(r\) by the equation, \(\left(P_{0}\right.\) is the atmospheric pressure & \(V\) is the final potential of the bubble