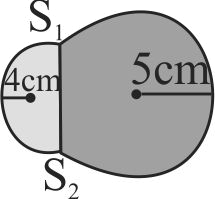
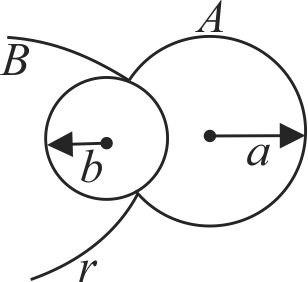
361229 A glass tube of uniform internal radius (\(r\)) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius \(r\). End 2 has sub-hemispherical soap bubble of radius \(r\) as shown in figure. Just after opening the valve.

361230 The excess pressure inside a spherical drop of water is four times that of another drop. Then their respective mass ratio is

361231 Two soap bubbles of radii \(r_{1}\) and \(r_{2}\) equal to \(4\;cm\) and \(5\;cm\) are touching each other over a common surface \({S_1}\;{S_2}\) (shown in figure ). Its radius will be

361232 Two soap bubbles coalesce. It is noticed that, whilst Joined together, the radii of the two bubbles are \(a\) and \(b\) where \(a>b\). Then, the radius of curvature of interface between the two bubbles will be

361229 A glass tube of uniform internal radius (\(r\)) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius \(r\). End 2 has sub-hemispherical soap bubble of radius \(r\) as shown in figure. Just after opening the valve.

361230 The excess pressure inside a spherical drop of water is four times that of another drop. Then their respective mass ratio is

361231 Two soap bubbles of radii \(r_{1}\) and \(r_{2}\) equal to \(4\;cm\) and \(5\;cm\) are touching each other over a common surface \({S_1}\;{S_2}\) (shown in figure ). Its radius will be

361232 Two soap bubbles coalesce. It is noticed that, whilst Joined together, the radii of the two bubbles are \(a\) and \(b\) where \(a>b\). Then, the radius of curvature of interface between the two bubbles will be

361229 A glass tube of uniform internal radius (\(r\)) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius \(r\). End 2 has sub-hemispherical soap bubble of radius \(r\) as shown in figure. Just after opening the valve.

361230 The excess pressure inside a spherical drop of water is four times that of another drop. Then their respective mass ratio is

361231 Two soap bubbles of radii \(r_{1}\) and \(r_{2}\) equal to \(4\;cm\) and \(5\;cm\) are touching each other over a common surface \({S_1}\;{S_2}\) (shown in figure ). Its radius will be

361232 Two soap bubbles coalesce. It is noticed that, whilst Joined together, the radii of the two bubbles are \(a\) and \(b\) where \(a>b\). Then, the radius of curvature of interface between the two bubbles will be

361229 A glass tube of uniform internal radius (\(r\)) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius \(r\). End 2 has sub-hemispherical soap bubble of radius \(r\) as shown in figure. Just after opening the valve.

361230 The excess pressure inside a spherical drop of water is four times that of another drop. Then their respective mass ratio is

361231 Two soap bubbles of radii \(r_{1}\) and \(r_{2}\) equal to \(4\;cm\) and \(5\;cm\) are touching each other over a common surface \({S_1}\;{S_2}\) (shown in figure ). Its radius will be

361232 Two soap bubbles coalesce. It is noticed that, whilst Joined together, the radii of the two bubbles are \(a\) and \(b\) where \(a>b\). Then, the radius of curvature of interface between the two bubbles will be