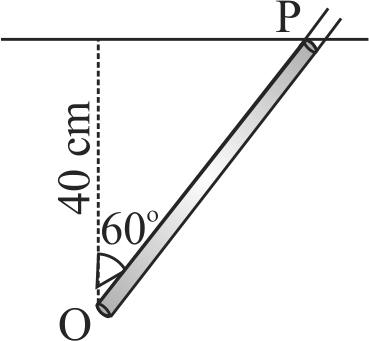
360980 A wooden rod of uniform cross-section and of length \(120\;cm\) is hinged at the bottom of the tank which is filled with water to a height of 40 \(cm\). In the equilibrium position, the rod makes an angle of \(60^{\circ}\) with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of :
360982
In the arrangement as shown, \(m_{B}=3 m\), density of liquid is \(\rho\) and density of block \(B\) is \(2 \rho\). The system is released from rest so that block \(B\) moves up when it is inside the liquid and moves down when it is outside of liquid with the same magnitude of acceleration. Find the mass of block \(A\).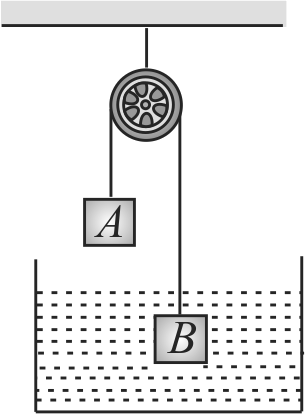
360983
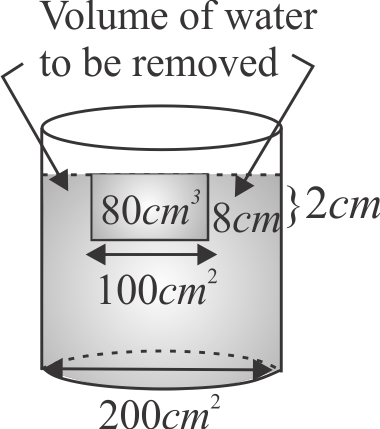
Figure shows a cubical block of side \(10\,cm\) and relative density 1.5 suspended by a wire of cross-sectional area \({10^{-6} {~m}^{2}}\). The breaking stress of the wire is \({7 \times 10^{6} {Nm}^{-2}}\). The block is placed in a beaker of base area \({200 {~cm}^{2}}\) and initially at \({t=0}\), the top surfaces of water and block coincide. There is a pump at the bottom corner, which ejects \({2 {~cm}^{3}}\) of water per second. If the time at which wire breaks is \({p \times 100}\) seconds, then the value of \({p}\) is
(Given, \({g=10 {~ms}^{-2}}\))
360980 A wooden rod of uniform cross-section and of length \(120\;cm\) is hinged at the bottom of the tank which is filled with water to a height of 40 \(cm\). In the equilibrium position, the rod makes an angle of \(60^{\circ}\) with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of :
360982
In the arrangement as shown, \(m_{B}=3 m\), density of liquid is \(\rho\) and density of block \(B\) is \(2 \rho\). The system is released from rest so that block \(B\) moves up when it is inside the liquid and moves down when it is outside of liquid with the same magnitude of acceleration. Find the mass of block \(A\).
360983
Figure shows a cubical block of side \(10\,cm\) and relative density 1.5 suspended by a wire of cross-sectional area \({10^{-6} {~m}^{2}}\). The breaking stress of the wire is \({7 \times 10^{6} {Nm}^{-2}}\). The block is placed in a beaker of base area \({200 {~cm}^{2}}\) and initially at \({t=0}\), the top surfaces of water and block coincide. There is a pump at the bottom corner, which ejects \({2 {~cm}^{3}}\) of water per second. If the time at which wire breaks is \({p \times 100}\) seconds, then the value of \({p}\) is
(Given, \({g=10 {~ms}^{-2}}\))
360980 A wooden rod of uniform cross-section and of length \(120\;cm\) is hinged at the bottom of the tank which is filled with water to a height of 40 \(cm\). In the equilibrium position, the rod makes an angle of \(60^{\circ}\) with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of :
360982
In the arrangement as shown, \(m_{B}=3 m\), density of liquid is \(\rho\) and density of block \(B\) is \(2 \rho\). The system is released from rest so that block \(B\) moves up when it is inside the liquid and moves down when it is outside of liquid with the same magnitude of acceleration. Find the mass of block \(A\).
360983
Figure shows a cubical block of side \(10\,cm\) and relative density 1.5 suspended by a wire of cross-sectional area \({10^{-6} {~m}^{2}}\). The breaking stress of the wire is \({7 \times 10^{6} {Nm}^{-2}}\). The block is placed in a beaker of base area \({200 {~cm}^{2}}\) and initially at \({t=0}\), the top surfaces of water and block coincide. There is a pump at the bottom corner, which ejects \({2 {~cm}^{3}}\) of water per second. If the time at which wire breaks is \({p \times 100}\) seconds, then the value of \({p}\) is
(Given, \({g=10 {~ms}^{-2}}\))
360980 A wooden rod of uniform cross-section and of length \(120\;cm\) is hinged at the bottom of the tank which is filled with water to a height of 40 \(cm\). In the equilibrium position, the rod makes an angle of \(60^{\circ}\) with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of :
360982
In the arrangement as shown, \(m_{B}=3 m\), density of liquid is \(\rho\) and density of block \(B\) is \(2 \rho\). The system is released from rest so that block \(B\) moves up when it is inside the liquid and moves down when it is outside of liquid with the same magnitude of acceleration. Find the mass of block \(A\).
360983
Figure shows a cubical block of side \(10\,cm\) and relative density 1.5 suspended by a wire of cross-sectional area \({10^{-6} {~m}^{2}}\). The breaking stress of the wire is \({7 \times 10^{6} {Nm}^{-2}}\). The block is placed in a beaker of base area \({200 {~cm}^{2}}\) and initially at \({t=0}\), the top surfaces of water and block coincide. There is a pump at the bottom corner, which ejects \({2 {~cm}^{3}}\) of water per second. If the time at which wire breaks is \({p \times 100}\) seconds, then the value of \({p}\) is
(Given, \({g=10 {~ms}^{-2}}\))