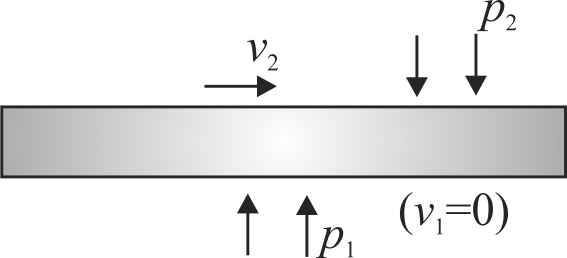
360821 Air is streaming past a horizontal aeroplane wing such that its speed is \(120\;\,m/s\) over the upper surface and \(90\;\,m/s\) at the lower surface. If the density of air is \(1.3\;\,kg/{m^3}\), then the difference of the pressure on the two sides of the wing is :-
360821 Air is streaming past a horizontal aeroplane wing such that its speed is \(120\;\,m/s\) over the upper surface and \(90\;\,m/s\) at the lower surface. If the density of air is \(1.3\;\,kg/{m^3}\), then the difference of the pressure on the two sides of the wing is :-
360821 Air is streaming past a horizontal aeroplane wing such that its speed is \(120\;\,m/s\) over the upper surface and \(90\;\,m/s\) at the lower surface. If the density of air is \(1.3\;\,kg/{m^3}\), then the difference of the pressure on the two sides of the wing is :-
360821 Air is streaming past a horizontal aeroplane wing such that its speed is \(120\;\,m/s\) over the upper surface and \(90\;\,m/s\) at the lower surface. If the density of air is \(1.3\;\,kg/{m^3}\), then the difference of the pressure on the two sides of the wing is :-