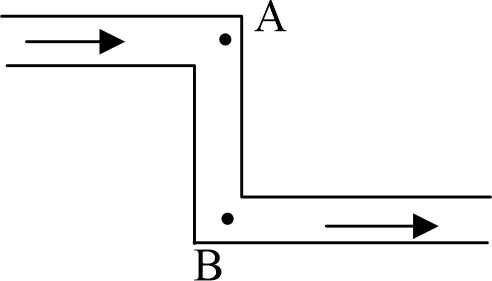
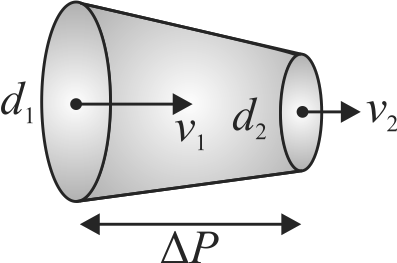
360810 Water is flowing with a velocity of \({2 {~m} / {s}}\) in a horizontal pipe where cross-sectional area is \({2 \times 10^{-2} {~m}^{2}}\) at pressure \({4 \times 10^{4} {~Pa}}\). The pressure (in \({P a}\) ) at cross-section of area \({0.01 m^{2}}\) will be
360810 Water is flowing with a velocity of \({2 {~m} / {s}}\) in a horizontal pipe where cross-sectional area is \({2 \times 10^{-2} {~m}^{2}}\) at pressure \({4 \times 10^{4} {~Pa}}\). The pressure (in \({P a}\) ) at cross-section of area \({0.01 m^{2}}\) will be
360810 Water is flowing with a velocity of \({2 {~m} / {s}}\) in a horizontal pipe where cross-sectional area is \({2 \times 10^{-2} {~m}^{2}}\) at pressure \({4 \times 10^{4} {~Pa}}\). The pressure (in \({P a}\) ) at cross-section of area \({0.01 m^{2}}\) will be
360810 Water is flowing with a velocity of \({2 {~m} / {s}}\) in a horizontal pipe where cross-sectional area is \({2 \times 10^{-2} {~m}^{2}}\) at pressure \({4 \times 10^{4} {~Pa}}\). The pressure (in \({P a}\) ) at cross-section of area \({0.01 m^{2}}\) will be
360810 Water is flowing with a velocity of \({2 {~m} / {s}}\) in a horizontal pipe where cross-sectional area is \({2 \times 10^{-2} {~m}^{2}}\) at pressure \({4 \times 10^{4} {~Pa}}\). The pressure (in \({P a}\) ) at cross-section of area \({0.01 m^{2}}\) will be