Explanation:
Let at point \(P\), magnetic field is zero
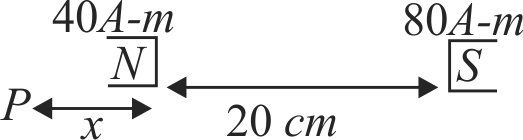
\(\therefore \dfrac{\mu_{0}}{4 \pi} \dfrac{m_{1}}{r_{1}^{2}}=\dfrac{\mu_{0}}{4 \pi} \dfrac{m_{2}}{r_{2}^{2}}\)
\(\frac{{40}}{{{x^2}}} = \frac{{80}}{{{{(20 + x)}^2}}}\;\;\;{\mkern 1mu} {\kern 1pt} [{\rm{from}}\,{\rm{figure}}]\)
\({(20 + x)^2} = 2{x^2}\)
\( \Rightarrow 20 + x = \sqrt 2 \,x\)
\(\therefore x = \frac{{20}}{{\sqrt 2 - 1}} = 48.2\;cm\)
\(\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{(towards}}\,\,{\rm{ north }}\,{\rm{pole)}}\)
So, correct option is (3)