Explanation:
Let \(m\) be the pole strength of the magnet. Let \(M\) and \(M^{\prime}\) be the magnetic moments when the magnet is in arc shape and straight shape respectively. Let \(\theta\) be the angle subtents by the arc at the centre.
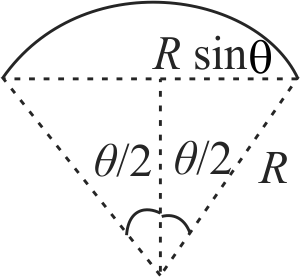
\(M = m\,2R\sin \left( {\frac{\theta }{2}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
\(2 R \sin \left(\dfrac{\theta}{2}\right)\) is the effective length of the magnet.
The arc length of the magnet is \(R \theta\). When the magnet is made straight then the magnetic moment is
\(M' = ml = m\,R\,\theta \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
From eqns \(1 \& 2\)
\(\dfrac{M}{M^{\prime}}=\dfrac{2 \sin \left(\dfrac{\theta}{2}\right)}{\theta}\)
Given that \(\theta=\dfrac{\pi}{2}\)
\(\dfrac{M}{M^{\prime}}=\dfrac{2 R \sin \left(\dfrac{\pi}{4}\right)}{\dfrac{\pi}{2}} \Rightarrow M^{\prime}=\dfrac{\pi M}{2 \sqrt{2}}\)