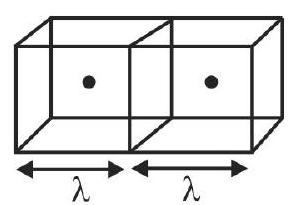
360313 Modern vaccum pumps can evacuate a vessel down to a pressure of \(4.0 \times {10^{ - 15}} atm\). At room temperature (300 K). Taking \(R = 8.0\,J{\rm{ }}{K^{ - 1}} mol{e^{ - 1}}\), \(1 atm = {10^5} Pa\) and \({N_{Avogadro{\rm{ }}}} = 6 \times {10^{23}} mol{e^{ - 1}}\), the mean distance between molecules of gas in an evacuated vessel will be of the order of:
360313 Modern vaccum pumps can evacuate a vessel down to a pressure of \(4.0 \times {10^{ - 15}} atm\). At room temperature (300 K). Taking \(R = 8.0\,J{\rm{ }}{K^{ - 1}} mol{e^{ - 1}}\), \(1 atm = {10^5} Pa\) and \({N_{Avogadro{\rm{ }}}} = 6 \times {10^{23}} mol{e^{ - 1}}\), the mean distance between molecules of gas in an evacuated vessel will be of the order of:
360313 Modern vaccum pumps can evacuate a vessel down to a pressure of \(4.0 \times {10^{ - 15}} atm\). At room temperature (300 K). Taking \(R = 8.0\,J{\rm{ }}{K^{ - 1}} mol{e^{ - 1}}\), \(1 atm = {10^5} Pa\) and \({N_{Avogadro{\rm{ }}}} = 6 \times {10^{23}} mol{e^{ - 1}}\), the mean distance between molecules of gas in an evacuated vessel will be of the order of:
360313 Modern vaccum pumps can evacuate a vessel down to a pressure of \(4.0 \times {10^{ - 15}} atm\). At room temperature (300 K). Taking \(R = 8.0\,J{\rm{ }}{K^{ - 1}} mol{e^{ - 1}}\), \(1 atm = {10^5} Pa\) and \({N_{Avogadro{\rm{ }}}} = 6 \times {10^{23}} mol{e^{ - 1}}\), the mean distance between molecules of gas in an evacuated vessel will be of the order of: