355660
In the figure, a block slides along a track from one level to a higher level, by moving through an intermediate valley. The track is frictionless untill the block reaches the higher level. There a frictional force stops the block in a distance \(d\). The block's initial speed \(v_{0}\) is \(6\;m{\rm{/}}s\), the height difference \(h\) is \(1.1\,m\) and the coefficient of kinetic friction \(\mu\) is 0.6 . The value of \(d\) is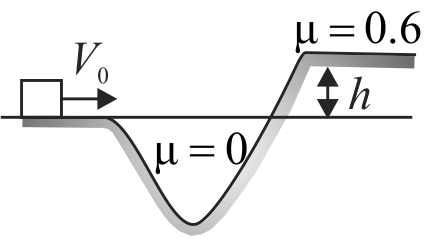
355660
In the figure, a block slides along a track from one level to a higher level, by moving through an intermediate valley. The track is frictionless untill the block reaches the higher level. There a frictional force stops the block in a distance \(d\). The block's initial speed \(v_{0}\) is \(6\;m{\rm{/}}s\), the height difference \(h\) is \(1.1\,m\) and the coefficient of kinetic friction \(\mu\) is 0.6 . The value of \(d\) is
355660
In the figure, a block slides along a track from one level to a higher level, by moving through an intermediate valley. The track is frictionless untill the block reaches the higher level. There a frictional force stops the block in a distance \(d\). The block's initial speed \(v_{0}\) is \(6\;m{\rm{/}}s\), the height difference \(h\) is \(1.1\,m\) and the coefficient of kinetic friction \(\mu\) is 0.6 . The value of \(d\) is
355660
In the figure, a block slides along a track from one level to a higher level, by moving through an intermediate valley. The track is frictionless untill the block reaches the higher level. There a frictional force stops the block in a distance \(d\). The block's initial speed \(v_{0}\) is \(6\;m{\rm{/}}s\), the height difference \(h\) is \(1.1\,m\) and the coefficient of kinetic friction \(\mu\) is 0.6 . The value of \(d\) is