355655
A small ball of mass \(m\) starts at a point \(A\) with speed \(\mathrm{v}_{0}\) and moves along a frictionless track \(AB\) as shown. The track \(BC\) has coefficient of friction \(\mu\). The ball comes to stop at \(C\) after travelling a distance \(L\) which is :-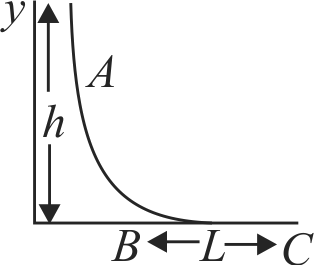
355657
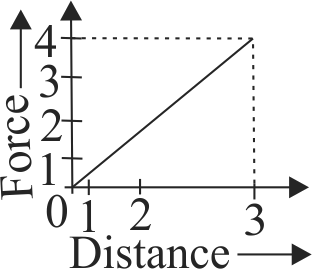
The graph between the resistive force \(F\) acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 2.5 \(kg\) and initial velocity is 2 \(m/s\). When the distance covered by the body is 4 \(m\) , its kinetic energy would be
355655
A small ball of mass \(m\) starts at a point \(A\) with speed \(\mathrm{v}_{0}\) and moves along a frictionless track \(AB\) as shown. The track \(BC\) has coefficient of friction \(\mu\). The ball comes to stop at \(C\) after travelling a distance \(L\) which is :-
355657
The graph between the resistive force \(F\) acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 2.5 \(kg\) and initial velocity is 2 \(m/s\). When the distance covered by the body is 4 \(m\) , its kinetic energy would be
355655
A small ball of mass \(m\) starts at a point \(A\) with speed \(\mathrm{v}_{0}\) and moves along a frictionless track \(AB\) as shown. The track \(BC\) has coefficient of friction \(\mu\). The ball comes to stop at \(C\) after travelling a distance \(L\) which is :-
355657
The graph between the resistive force \(F\) acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 2.5 \(kg\) and initial velocity is 2 \(m/s\). When the distance covered by the body is 4 \(m\) , its kinetic energy would be
355655
A small ball of mass \(m\) starts at a point \(A\) with speed \(\mathrm{v}_{0}\) and moves along a frictionless track \(AB\) as shown. The track \(BC\) has coefficient of friction \(\mu\). The ball comes to stop at \(C\) after travelling a distance \(L\) which is :-
355657
The graph between the resistive force \(F\) acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 2.5 \(kg\) and initial velocity is 2 \(m/s\). When the distance covered by the body is 4 \(m\) , its kinetic energy would be
355655
A small ball of mass \(m\) starts at a point \(A\) with speed \(\mathrm{v}_{0}\) and moves along a frictionless track \(AB\) as shown. The track \(BC\) has coefficient of friction \(\mu\). The ball comes to stop at \(C\) after travelling a distance \(L\) which is :-
355657
The graph between the resistive force \(F\) acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 2.5 \(kg\) and initial velocity is 2 \(m/s\). When the distance covered by the body is 4 \(m\) , its kinetic energy would be