355647 A particle of mass 0.01 \(kg\) travels with velocity given by \((4\widehat {\rm{i}} + 16)km{s^{ - 1}}\). After sometime, its velocity becomes \((8\widehat i + 20)\widehat j\,m{s^{ - 1}}\). The work done on particle during this interval of time is

355648 A body of mass \(10\;kg\) initially at rest acquires velocity \(10\;m{s^{ - 1}}.\) What is the work done?

355649 A long block \(A\) is at rest on a smooth horizontal surface. A small block \(B\) whose mass is half mass of \(A\) is placed on \(A\) at one end and is given an initial velocity u as shown in the figure. The coefficient of friction between the blocks is \(\mu\)

355650 A dog of mass \(m = 4\;kg\) runs from the left end of a curved ramp with speed \({V_0} = 8\;m{\rm{/}}s\) at height \(8\;m\) above the ground. It then slides to the right and comes to rest when it reaches a height \(10\;m\) from the ground. The maximum increase in thermal energy of the dog-ramp system because of sliding is \(\left( {g = 10\;m{\rm{/}}{s^2}} \right)\)

355647 A particle of mass 0.01 \(kg\) travels with velocity given by \((4\widehat {\rm{i}} + 16)km{s^{ - 1}}\). After sometime, its velocity becomes \((8\widehat i + 20)\widehat j\,m{s^{ - 1}}\). The work done on particle during this interval of time is

355648 A body of mass \(10\;kg\) initially at rest acquires velocity \(10\;m{s^{ - 1}}.\) What is the work done?

355649 A long block \(A\) is at rest on a smooth horizontal surface. A small block \(B\) whose mass is half mass of \(A\) is placed on \(A\) at one end and is given an initial velocity u as shown in the figure. The coefficient of friction between the blocks is \(\mu\)

355650 A dog of mass \(m = 4\;kg\) runs from the left end of a curved ramp with speed \({V_0} = 8\;m{\rm{/}}s\) at height \(8\;m\) above the ground. It then slides to the right and comes to rest when it reaches a height \(10\;m\) from the ground. The maximum increase in thermal energy of the dog-ramp system because of sliding is \(\left( {g = 10\;m{\rm{/}}{s^2}} \right)\)

355647 A particle of mass 0.01 \(kg\) travels with velocity given by \((4\widehat {\rm{i}} + 16)km{s^{ - 1}}\). After sometime, its velocity becomes \((8\widehat i + 20)\widehat j\,m{s^{ - 1}}\). The work done on particle during this interval of time is

355648 A body of mass \(10\;kg\) initially at rest acquires velocity \(10\;m{s^{ - 1}}.\) What is the work done?

355649 A long block \(A\) is at rest on a smooth horizontal surface. A small block \(B\) whose mass is half mass of \(A\) is placed on \(A\) at one end and is given an initial velocity u as shown in the figure. The coefficient of friction between the blocks is \(\mu\)

355650 A dog of mass \(m = 4\;kg\) runs from the left end of a curved ramp with speed \({V_0} = 8\;m{\rm{/}}s\) at height \(8\;m\) above the ground. It then slides to the right and comes to rest when it reaches a height \(10\;m\) from the ground. The maximum increase in thermal energy of the dog-ramp system because of sliding is \(\left( {g = 10\;m{\rm{/}}{s^2}} \right)\)

355647 A particle of mass 0.01 \(kg\) travels with velocity given by \((4\widehat {\rm{i}} + 16)km{s^{ - 1}}\). After sometime, its velocity becomes \((8\widehat i + 20)\widehat j\,m{s^{ - 1}}\). The work done on particle during this interval of time is

355648 A body of mass \(10\;kg\) initially at rest acquires velocity \(10\;m{s^{ - 1}}.\) What is the work done?

355649 A long block \(A\) is at rest on a smooth horizontal surface. A small block \(B\) whose mass is half mass of \(A\) is placed on \(A\) at one end and is given an initial velocity u as shown in the figure. The coefficient of friction between the blocks is \(\mu\)

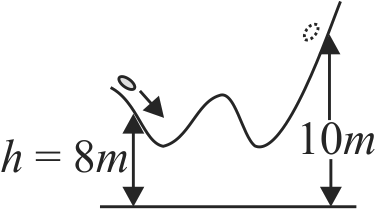
355650 A dog of mass \(m = 4\;kg\) runs from the left end of a curved ramp with speed \({V_0} = 8\;m{\rm{/}}s\) at height \(8\;m\) above the ground. It then slides to the right and comes to rest when it reaches a height \(10\;m\) from the ground. The maximum increase in thermal energy of the dog-ramp system because of sliding is \(\left( {g = 10\;m{\rm{/}}{s^2}} \right)\)