355632 A particle of mass \(m\) moves on a straight line with its velocity increasing with distance according to the equation \(v=\alpha \sqrt{x}\), where \(\alpha\) is a constant. The total work done by all the forces applied on the particle during its displacement from \(x=0\) to \(x=d\), will be
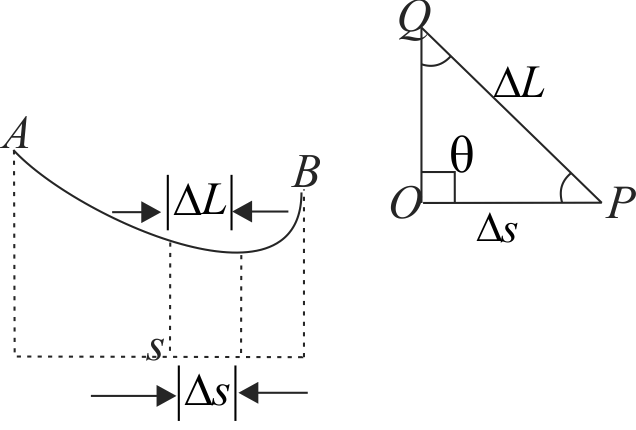
355633 A skier starts from rest at point \(A\) and slides down the hill without turning or breaking. The friction coefficient is \(\mu\). When he stops at point \(B\), his horizontal displacement is \(s\). What is the height difference between points \(A\) and \(B\) ? (The velocity of the skier is small, so that the additional pressure on the snow due to the curvature can be neglected. Neglect also the friction of air and the dependence of \(\mu\) on the velocity of the skier.)
355632 A particle of mass \(m\) moves on a straight line with its velocity increasing with distance according to the equation \(v=\alpha \sqrt{x}\), where \(\alpha\) is a constant. The total work done by all the forces applied on the particle during its displacement from \(x=0\) to \(x=d\), will be
355633 A skier starts from rest at point \(A\) and slides down the hill without turning or breaking. The friction coefficient is \(\mu\). When he stops at point \(B\), his horizontal displacement is \(s\). What is the height difference between points \(A\) and \(B\) ? (The velocity of the skier is small, so that the additional pressure on the snow due to the curvature can be neglected. Neglect also the friction of air and the dependence of \(\mu\) on the velocity of the skier.)
355632 A particle of mass \(m\) moves on a straight line with its velocity increasing with distance according to the equation \(v=\alpha \sqrt{x}\), where \(\alpha\) is a constant. The total work done by all the forces applied on the particle during its displacement from \(x=0\) to \(x=d\), will be
355633 A skier starts from rest at point \(A\) and slides down the hill without turning or breaking. The friction coefficient is \(\mu\). When he stops at point \(B\), his horizontal displacement is \(s\). What is the height difference between points \(A\) and \(B\) ? (The velocity of the skier is small, so that the additional pressure on the snow due to the curvature can be neglected. Neglect also the friction of air and the dependence of \(\mu\) on the velocity of the skier.)
355632 A particle of mass \(m\) moves on a straight line with its velocity increasing with distance according to the equation \(v=\alpha \sqrt{x}\), where \(\alpha\) is a constant. The total work done by all the forces applied on the particle during its displacement from \(x=0\) to \(x=d\), will be
355633 A skier starts from rest at point \(A\) and slides down the hill without turning or breaking. The friction coefficient is \(\mu\). When he stops at point \(B\), his horizontal displacement is \(s\). What is the height difference between points \(A\) and \(B\) ? (The velocity of the skier is small, so that the additional pressure on the snow due to the curvature can be neglected. Neglect also the friction of air and the dependence of \(\mu\) on the velocity of the skier.)