355627
Consider an elliptically shaped rail \(PQ\) in the vertical plane with \(OP = 6\;m\) and \(OQ = 8\;m\). A block of mass \(1\;kg\) is pulled along the rail from \(P\) to \(Q\) with a force of \(15\;N,\) which is always parallel to line \(PQ\) (see the figure given).
Assuming no frictional losses, the kinetic energy of the block when it reaches \(Q\) is \((n \times 10)\) joules.
The value of \(n\) is
(Take acceleration due to gravity \( = 10\;m{{\rm{s}}^{ - 2}}\))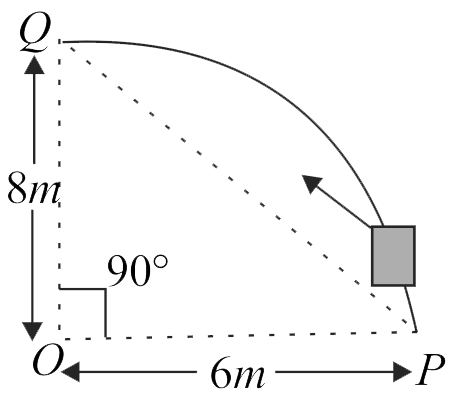
355627
Consider an elliptically shaped rail \(PQ\) in the vertical plane with \(OP = 6\;m\) and \(OQ = 8\;m\). A block of mass \(1\;kg\) is pulled along the rail from \(P\) to \(Q\) with a force of \(15\;N,\) which is always parallel to line \(PQ\) (see the figure given).
Assuming no frictional losses, the kinetic energy of the block when it reaches \(Q\) is \((n \times 10)\) joules.
The value of \(n\) is
(Take acceleration due to gravity \( = 10\;m{{\rm{s}}^{ - 2}}\))
355627
Consider an elliptically shaped rail \(PQ\) in the vertical plane with \(OP = 6\;m\) and \(OQ = 8\;m\). A block of mass \(1\;kg\) is pulled along the rail from \(P\) to \(Q\) with a force of \(15\;N,\) which is always parallel to line \(PQ\) (see the figure given).
Assuming no frictional losses, the kinetic energy of the block when it reaches \(Q\) is \((n \times 10)\) joules.
The value of \(n\) is
(Take acceleration due to gravity \( = 10\;m{{\rm{s}}^{ - 2}}\))
355627
Consider an elliptically shaped rail \(PQ\) in the vertical plane with \(OP = 6\;m\) and \(OQ = 8\;m\). A block of mass \(1\;kg\) is pulled along the rail from \(P\) to \(Q\) with a force of \(15\;N,\) which is always parallel to line \(PQ\) (see the figure given).
Assuming no frictional losses, the kinetic energy of the block when it reaches \(Q\) is \((n \times 10)\) joules.
The value of \(n\) is
(Take acceleration due to gravity \( = 10\;m{{\rm{s}}^{ - 2}}\))
355627
Consider an elliptically shaped rail \(PQ\) in the vertical plane with \(OP = 6\;m\) and \(OQ = 8\;m\). A block of mass \(1\;kg\) is pulled along the rail from \(P\) to \(Q\) with a force of \(15\;N,\) which is always parallel to line \(PQ\) (see the figure given).
Assuming no frictional losses, the kinetic energy of the block when it reaches \(Q\) is \((n \times 10)\) joules.
The value of \(n\) is
(Take acceleration due to gravity \( = 10\;m{{\rm{s}}^{ - 2}}\))