355615
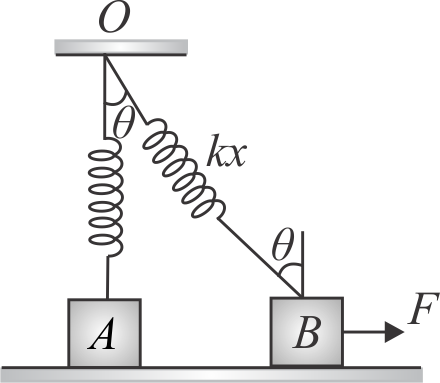
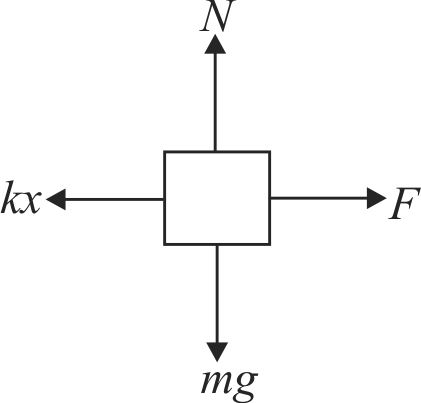
In the situation in figure, a block of mass \(1\,kg\) is attached to a light spring of constant \({40 {~N} / {m}}\) whose other end is fixed to the roof of a building \(50\,cm\) above the smooth horizontal surface. Initially, spring is in natural length and vertical. When a force \({F=20 \sqrt{3} {~N}}\) is applied on the block, the block starts to move. The speed at the instant it breaks off the surface below it is \({\sqrt{10 n} {~m} / {s}}\). The value of \({n}\) is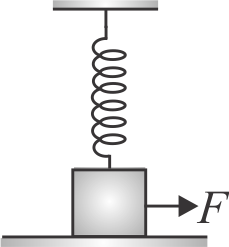
355617
A block of mass \(1\,kg\) is released from top of a rough incline having \({\mu=\dfrac{1}{\sqrt{3}}}\). The initial speed of block is \({2 {~m} / {s}}\). The incline plane is of unknown length and has a spring of constant \({k=1 {~N} / {m}}\) connected at base as in figure. Find the maximum compression of spring.
355618
The figure shows a mass \(m\) on a frictonless surface. It is connected to rigid wall by the mean of a mass-less spring of its constant \(k\). Initially, the spring is at its natural position. If a force of constant magnitude starts acting on the block towards right, then the speed of the block when the deformation in spring is \(x\), will be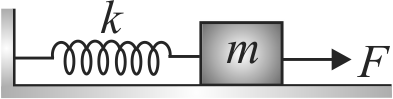
355615
In the situation in figure, a block of mass \(1\,kg\) is attached to a light spring of constant \({40 {~N} / {m}}\) whose other end is fixed to the roof of a building \(50\,cm\) above the smooth horizontal surface. Initially, spring is in natural length and vertical. When a force \({F=20 \sqrt{3} {~N}}\) is applied on the block, the block starts to move. The speed at the instant it breaks off the surface below it is \({\sqrt{10 n} {~m} / {s}}\). The value of \({n}\) is
355617
A block of mass \(1\,kg\) is released from top of a rough incline having \({\mu=\dfrac{1}{\sqrt{3}}}\). The initial speed of block is \({2 {~m} / {s}}\). The incline plane is of unknown length and has a spring of constant \({k=1 {~N} / {m}}\) connected at base as in figure. Find the maximum compression of spring.
355618
The figure shows a mass \(m\) on a frictonless surface. It is connected to rigid wall by the mean of a mass-less spring of its constant \(k\). Initially, the spring is at its natural position. If a force of constant magnitude starts acting on the block towards right, then the speed of the block when the deformation in spring is \(x\), will be
355615
In the situation in figure, a block of mass \(1\,kg\) is attached to a light spring of constant \({40 {~N} / {m}}\) whose other end is fixed to the roof of a building \(50\,cm\) above the smooth horizontal surface. Initially, spring is in natural length and vertical. When a force \({F=20 \sqrt{3} {~N}}\) is applied on the block, the block starts to move. The speed at the instant it breaks off the surface below it is \({\sqrt{10 n} {~m} / {s}}\). The value of \({n}\) is
355617
A block of mass \(1\,kg\) is released from top of a rough incline having \({\mu=\dfrac{1}{\sqrt{3}}}\). The initial speed of block is \({2 {~m} / {s}}\). The incline plane is of unknown length and has a spring of constant \({k=1 {~N} / {m}}\) connected at base as in figure. Find the maximum compression of spring.
355618
The figure shows a mass \(m\) on a frictonless surface. It is connected to rigid wall by the mean of a mass-less spring of its constant \(k\). Initially, the spring is at its natural position. If a force of constant magnitude starts acting on the block towards right, then the speed of the block when the deformation in spring is \(x\), will be
355615
In the situation in figure, a block of mass \(1\,kg\) is attached to a light spring of constant \({40 {~N} / {m}}\) whose other end is fixed to the roof of a building \(50\,cm\) above the smooth horizontal surface. Initially, spring is in natural length and vertical. When a force \({F=20 \sqrt{3} {~N}}\) is applied on the block, the block starts to move. The speed at the instant it breaks off the surface below it is \({\sqrt{10 n} {~m} / {s}}\). The value of \({n}\) is
355617
A block of mass \(1\,kg\) is released from top of a rough incline having \({\mu=\dfrac{1}{\sqrt{3}}}\). The initial speed of block is \({2 {~m} / {s}}\). The incline plane is of unknown length and has a spring of constant \({k=1 {~N} / {m}}\) connected at base as in figure. Find the maximum compression of spring.
355618
The figure shows a mass \(m\) on a frictonless surface. It is connected to rigid wall by the mean of a mass-less spring of its constant \(k\). Initially, the spring is at its natural position. If a force of constant magnitude starts acting on the block towards right, then the speed of the block when the deformation in spring is \(x\), will be