355585
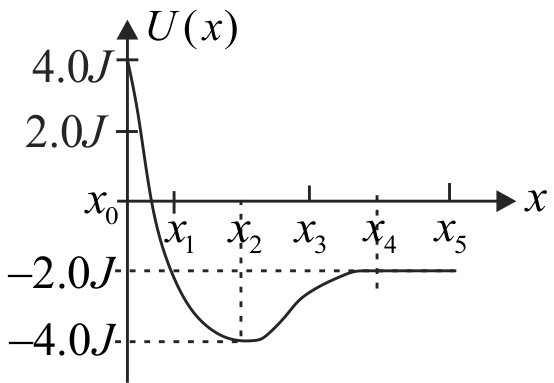
The potential energy function \(U\left( x \right)\) is associated with a conservative force \(F\) and described by the graph given above. If a particle being acted upon by this force has a kinetic energy of \(1.0\,J\) at position \({x_0}\). What is the particle’s kinetic energy at position \({x_4}\)?
355585

The potential energy function \(U\left( x \right)\) is associated with a conservative force \(F\) and described by the graph given above. If a particle being acted upon by this force has a kinetic energy of \(1.0\,J\) at position \({x_0}\). What is the particle’s kinetic energy at position \({x_4}\)?
355585

The potential energy function \(U\left( x \right)\) is associated with a conservative force \(F\) and described by the graph given above. If a particle being acted upon by this force has a kinetic energy of \(1.0\,J\) at position \({x_0}\). What is the particle’s kinetic energy at position \({x_4}\)?
355585

The potential energy function \(U\left( x \right)\) is associated with a conservative force \(F\) and described by the graph given above. If a particle being acted upon by this force has a kinetic energy of \(1.0\,J\) at position \({x_0}\). What is the particle’s kinetic energy at position \({x_4}\)?
