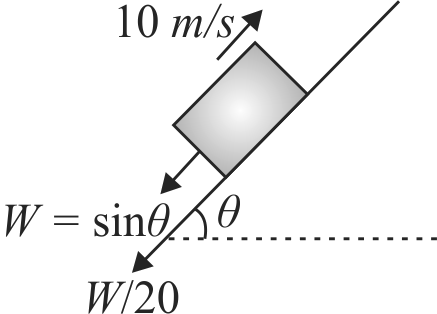
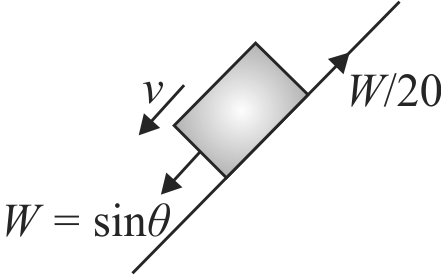
355467 A car of weight \(W\) is on an inclined road that rises by 100 \(m\) over a distance of 1 \(km\) and applies a constant frictional force \(\frac{W}{{20}}\) on the car. While moving uphill on the road at a speed of \(10\;m/s\), 1 the car needs power \(P\). If it needs power \(\dfrac{P}{2}\) while moving downhill at speed \(v\) then value of \(v\) is :

355468 A particle of mass \({\dfrac{10}{7} {~kg}}\) is moving in the positive \({x}\)-direction. Its initial position is \({x=0}\) and initial velocity is \({1 {~m} / {s}}\). The velocity at \({x=10 m}\) is (use the graph given)

355469 A force \({F}\) acting on a body depends on its displacement \({s}\) as \({F \propto s^{-1 / 3}}\). The power delivered by \({F}\) will depend on displacement as

355470 A car of mass \({m}\) is accelerating on a smooth level road under a single force \({F}\). The power delivered to the car is constant and equal to \({P}\). If the car's velocity at an instant is \({v}\), then after traveling how much distance, it gets doubled?

355467 A car of weight \(W\) is on an inclined road that rises by 100 \(m\) over a distance of 1 \(km\) and applies a constant frictional force \(\frac{W}{{20}}\) on the car. While moving uphill on the road at a speed of \(10\;m/s\), 1 the car needs power \(P\). If it needs power \(\dfrac{P}{2}\) while moving downhill at speed \(v\) then value of \(v\) is :

355468 A particle of mass \({\dfrac{10}{7} {~kg}}\) is moving in the positive \({x}\)-direction. Its initial position is \({x=0}\) and initial velocity is \({1 {~m} / {s}}\). The velocity at \({x=10 m}\) is (use the graph given)

355469 A force \({F}\) acting on a body depends on its displacement \({s}\) as \({F \propto s^{-1 / 3}}\). The power delivered by \({F}\) will depend on displacement as

355470 A car of mass \({m}\) is accelerating on a smooth level road under a single force \({F}\). The power delivered to the car is constant and equal to \({P}\). If the car's velocity at an instant is \({v}\), then after traveling how much distance, it gets doubled?

355467 A car of weight \(W\) is on an inclined road that rises by 100 \(m\) over a distance of 1 \(km\) and applies a constant frictional force \(\frac{W}{{20}}\) on the car. While moving uphill on the road at a speed of \(10\;m/s\), 1 the car needs power \(P\). If it needs power \(\dfrac{P}{2}\) while moving downhill at speed \(v\) then value of \(v\) is :

355468 A particle of mass \({\dfrac{10}{7} {~kg}}\) is moving in the positive \({x}\)-direction. Its initial position is \({x=0}\) and initial velocity is \({1 {~m} / {s}}\). The velocity at \({x=10 m}\) is (use the graph given)

355469 A force \({F}\) acting on a body depends on its displacement \({s}\) as \({F \propto s^{-1 / 3}}\). The power delivered by \({F}\) will depend on displacement as

355470 A car of mass \({m}\) is accelerating on a smooth level road under a single force \({F}\). The power delivered to the car is constant and equal to \({P}\). If the car's velocity at an instant is \({v}\), then after traveling how much distance, it gets doubled?

355467 A car of weight \(W\) is on an inclined road that rises by 100 \(m\) over a distance of 1 \(km\) and applies a constant frictional force \(\frac{W}{{20}}\) on the car. While moving uphill on the road at a speed of \(10\;m/s\), 1 the car needs power \(P\). If it needs power \(\dfrac{P}{2}\) while moving downhill at speed \(v\) then value of \(v\) is :

355468 A particle of mass \({\dfrac{10}{7} {~kg}}\) is moving in the positive \({x}\)-direction. Its initial position is \({x=0}\) and initial velocity is \({1 {~m} / {s}}\). The velocity at \({x=10 m}\) is (use the graph given)

355469 A force \({F}\) acting on a body depends on its displacement \({s}\) as \({F \propto s^{-1 / 3}}\). The power delivered by \({F}\) will depend on displacement as

355470 A car of mass \({m}\) is accelerating on a smooth level road under a single force \({F}\). The power delivered to the car is constant and equal to \({P}\). If the car's velocity at an instant is \({v}\), then after traveling how much distance, it gets doubled?