355295
Two pendulums each of length \(l\) are initially situated as shown in the figure. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?
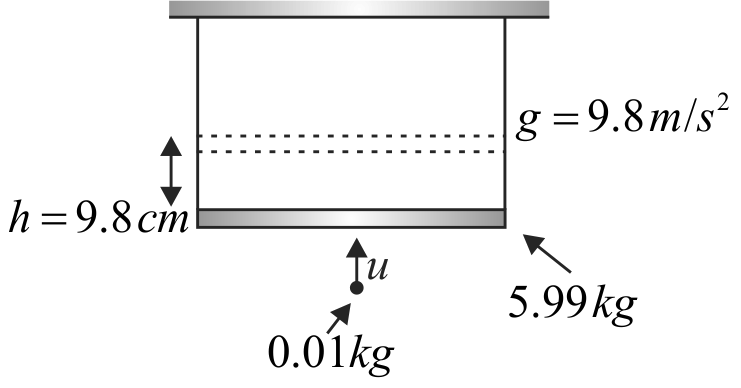
355296 A bullet of mass 10 \(g\) moving horizontally with a velocity of \(400\;m{s^{ - 1}}\) strikes a wooden block of mass \(2\;kg\) which is suspended by a light inextensible string of length 5 \(m\). As a result, the centre of gravity of the block is found to rise a vertical distance of 10 \(cm\). The speed of the bullet after it emerges out horizontally from the block will be
355295
Two pendulums each of length \(l\) are initially situated as shown in the figure. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?
355296 A bullet of mass 10 \(g\) moving horizontally with a velocity of \(400\;m{s^{ - 1}}\) strikes a wooden block of mass \(2\;kg\) which is suspended by a light inextensible string of length 5 \(m\). As a result, the centre of gravity of the block is found to rise a vertical distance of 10 \(cm\). The speed of the bullet after it emerges out horizontally from the block will be
355295
Two pendulums each of length \(l\) are initially situated as shown in the figure. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?
355296 A bullet of mass 10 \(g\) moving horizontally with a velocity of \(400\;m{s^{ - 1}}\) strikes a wooden block of mass \(2\;kg\) which is suspended by a light inextensible string of length 5 \(m\). As a result, the centre of gravity of the block is found to rise a vertical distance of 10 \(cm\). The speed of the bullet after it emerges out horizontally from the block will be
355295
Two pendulums each of length \(l\) are initially situated as shown in the figure. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?
355296 A bullet of mass 10 \(g\) moving horizontally with a velocity of \(400\;m{s^{ - 1}}\) strikes a wooden block of mass \(2\;kg\) which is suspended by a light inextensible string of length 5 \(m\). As a result, the centre of gravity of the block is found to rise a vertical distance of 10 \(cm\). The speed of the bullet after it emerges out horizontally from the block will be
355295
Two pendulums each of length \(l\) are initially situated as shown in the figure. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?
355296 A bullet of mass 10 \(g\) moving horizontally with a velocity of \(400\;m{s^{ - 1}}\) strikes a wooden block of mass \(2\;kg\) which is suspended by a light inextensible string of length 5 \(m\). As a result, the centre of gravity of the block is found to rise a vertical distance of 10 \(cm\). The speed of the bullet after it emerges out horizontally from the block will be