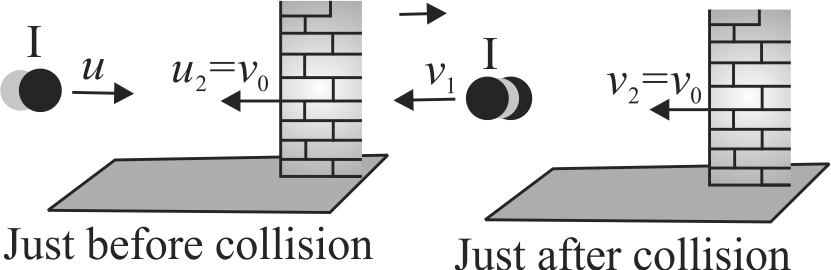
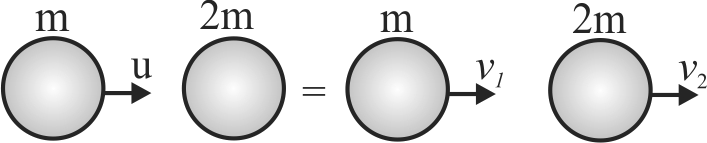
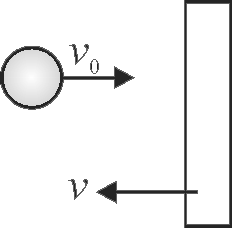
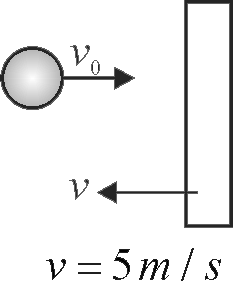
355286 A particle is moving with velocity \(u=2 {~m} / {s}\) towards a heavy wall moving towards the particle with constant speed \(v_{0}=1 {~m} / {s}\) as shown in the figure. Assuming collision to be elastic, find the velocity of the particle immediately after the collision.

355287 A particle of mass ' \({m}\) ' is moving horizontally \({w i}\) th a speed ' \({v}\) ' towards a rigid wall which is moving in the opposite direction with a constant velocity \({u}\). Assuming elastic impact between the wall and the particle, the work done by the wall in reflecting the particle is :

355288 A ball of mass \(m\) is moving with velocity \(u\) towards another stationary ball of mass 2 \(m\). If collision is elastic then the percentage \(KE\) transferred by ball 1 to ball 2 is

355289 A particle of mass \({m}\) moves with \({a}\) velocity of \({v_{0}=20 {~m} / {s}}\) towards a wall, which is moving with velocity \({v=5 {~m} / {s}}\). If the particle collides with the wall elastically, the speed of the particle just after the collision is

355286 A particle is moving with velocity \(u=2 {~m} / {s}\) towards a heavy wall moving towards the particle with constant speed \(v_{0}=1 {~m} / {s}\) as shown in the figure. Assuming collision to be elastic, find the velocity of the particle immediately after the collision.

355287 A particle of mass ' \({m}\) ' is moving horizontally \({w i}\) th a speed ' \({v}\) ' towards a rigid wall which is moving in the opposite direction with a constant velocity \({u}\). Assuming elastic impact between the wall and the particle, the work done by the wall in reflecting the particle is :

355288 A ball of mass \(m\) is moving with velocity \(u\) towards another stationary ball of mass 2 \(m\). If collision is elastic then the percentage \(KE\) transferred by ball 1 to ball 2 is

355289 A particle of mass \({m}\) moves with \({a}\) velocity of \({v_{0}=20 {~m} / {s}}\) towards a wall, which is moving with velocity \({v=5 {~m} / {s}}\). If the particle collides with the wall elastically, the speed of the particle just after the collision is

355286 A particle is moving with velocity \(u=2 {~m} / {s}\) towards a heavy wall moving towards the particle with constant speed \(v_{0}=1 {~m} / {s}\) as shown in the figure. Assuming collision to be elastic, find the velocity of the particle immediately after the collision.

355287 A particle of mass ' \({m}\) ' is moving horizontally \({w i}\) th a speed ' \({v}\) ' towards a rigid wall which is moving in the opposite direction with a constant velocity \({u}\). Assuming elastic impact between the wall and the particle, the work done by the wall in reflecting the particle is :

355288 A ball of mass \(m\) is moving with velocity \(u\) towards another stationary ball of mass 2 \(m\). If collision is elastic then the percentage \(KE\) transferred by ball 1 to ball 2 is

355289 A particle of mass \({m}\) moves with \({a}\) velocity of \({v_{0}=20 {~m} / {s}}\) towards a wall, which is moving with velocity \({v=5 {~m} / {s}}\). If the particle collides with the wall elastically, the speed of the particle just after the collision is

355286 A particle is moving with velocity \(u=2 {~m} / {s}\) towards a heavy wall moving towards the particle with constant speed \(v_{0}=1 {~m} / {s}\) as shown in the figure. Assuming collision to be elastic, find the velocity of the particle immediately after the collision.

355287 A particle of mass ' \({m}\) ' is moving horizontally \({w i}\) th a speed ' \({v}\) ' towards a rigid wall which is moving in the opposite direction with a constant velocity \({u}\). Assuming elastic impact between the wall and the particle, the work done by the wall in reflecting the particle is :

355288 A ball of mass \(m\) is moving with velocity \(u\) towards another stationary ball of mass 2 \(m\). If collision is elastic then the percentage \(KE\) transferred by ball 1 to ball 2 is

355289 A particle of mass \({m}\) moves with \({a}\) velocity of \({v_{0}=20 {~m} / {s}}\) towards a wall, which is moving with velocity \({v=5 {~m} / {s}}\). If the particle collides with the wall elastically, the speed of the particle just after the collision is