355277
Assertion :
In an elastic collision of two billiard balls, the total kinetic energy is conserved during the short time of oscillation of the balls (i.e., when they are in contact).
Reason :
Energy spent against friction does not follow the law of conservation of energy.
355278
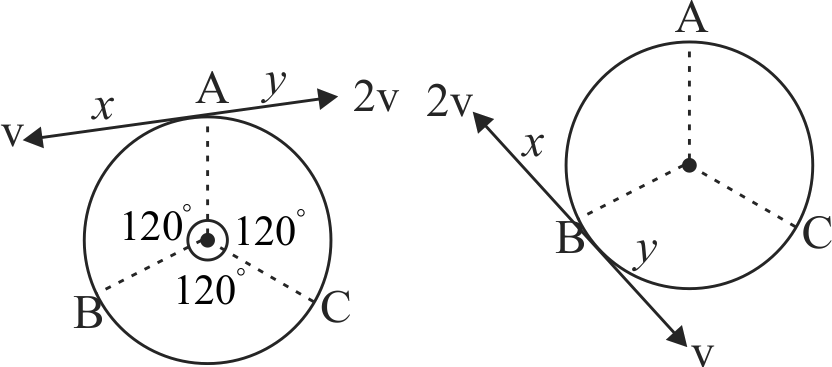
Two small particles of each mass \(m\) start moving in opposite direction from a point \(A\) in a horizontal circular orbit. Their tangential velocities are \(v\) and \(2 v\) respectively as shown in the figure between collisions, the particles move with constant speeds. After making how many elastic collision other than that at \(A\). These two particles will again reach the point \(A\)
355279
Assertion :
\(n\) small balls (per second) (each of mass \(m\) ) are colliding elastically with vertical surface with velocity \(u\). The force experienced by the surface is \(2\,mnu\).
Reason :
On elastic collision, in this case, the ball rebounds with the same velocity.
355280 A particle of mass \(m\) moves towards a smooth vertical wall with a speed \(u\) (relative to the ground) and collides elastically with the wall, the wall moving towards the particle with a speed 2 \(u\) (also relative to the ground). Assuming that the wall is extremely massive, the impulse delivered to the particle equals.
355277
Assertion :
In an elastic collision of two billiard balls, the total kinetic energy is conserved during the short time of oscillation of the balls (i.e., when they are in contact).
Reason :
Energy spent against friction does not follow the law of conservation of energy.
355278
Two small particles of each mass \(m\) start moving in opposite direction from a point \(A\) in a horizontal circular orbit. Their tangential velocities are \(v\) and \(2 v\) respectively as shown in the figure between collisions, the particles move with constant speeds. After making how many elastic collision other than that at \(A\). These two particles will again reach the point \(A\)
355279
Assertion :
\(n\) small balls (per second) (each of mass \(m\) ) are colliding elastically with vertical surface with velocity \(u\). The force experienced by the surface is \(2\,mnu\).
Reason :
On elastic collision, in this case, the ball rebounds with the same velocity.
355280 A particle of mass \(m\) moves towards a smooth vertical wall with a speed \(u\) (relative to the ground) and collides elastically with the wall, the wall moving towards the particle with a speed 2 \(u\) (also relative to the ground). Assuming that the wall is extremely massive, the impulse delivered to the particle equals.
355277
Assertion :
In an elastic collision of two billiard balls, the total kinetic energy is conserved during the short time of oscillation of the balls (i.e., when they are in contact).
Reason :
Energy spent against friction does not follow the law of conservation of energy.
355278
Two small particles of each mass \(m\) start moving in opposite direction from a point \(A\) in a horizontal circular orbit. Their tangential velocities are \(v\) and \(2 v\) respectively as shown in the figure between collisions, the particles move with constant speeds. After making how many elastic collision other than that at \(A\). These two particles will again reach the point \(A\)
355279
Assertion :
\(n\) small balls (per second) (each of mass \(m\) ) are colliding elastically with vertical surface with velocity \(u\). The force experienced by the surface is \(2\,mnu\).
Reason :
On elastic collision, in this case, the ball rebounds with the same velocity.
355280 A particle of mass \(m\) moves towards a smooth vertical wall with a speed \(u\) (relative to the ground) and collides elastically with the wall, the wall moving towards the particle with a speed 2 \(u\) (also relative to the ground). Assuming that the wall is extremely massive, the impulse delivered to the particle equals.
355277
Assertion :
In an elastic collision of two billiard balls, the total kinetic energy is conserved during the short time of oscillation of the balls (i.e., when they are in contact).
Reason :
Energy spent against friction does not follow the law of conservation of energy.
355278
Two small particles of each mass \(m\) start moving in opposite direction from a point \(A\) in a horizontal circular orbit. Their tangential velocities are \(v\) and \(2 v\) respectively as shown in the figure between collisions, the particles move with constant speeds. After making how many elastic collision other than that at \(A\). These two particles will again reach the point \(A\)
355279
Assertion :
\(n\) small balls (per second) (each of mass \(m\) ) are colliding elastically with vertical surface with velocity \(u\). The force experienced by the surface is \(2\,mnu\).
Reason :
On elastic collision, in this case, the ball rebounds with the same velocity.
355280 A particle of mass \(m\) moves towards a smooth vertical wall with a speed \(u\) (relative to the ground) and collides elastically with the wall, the wall moving towards the particle with a speed 2 \(u\) (also relative to the ground). Assuming that the wall is extremely massive, the impulse delivered to the particle equals.
355277
Assertion :
In an elastic collision of two billiard balls, the total kinetic energy is conserved during the short time of oscillation of the balls (i.e., when they are in contact).
Reason :
Energy spent against friction does not follow the law of conservation of energy.
355278
Two small particles of each mass \(m\) start moving in opposite direction from a point \(A\) in a horizontal circular orbit. Their tangential velocities are \(v\) and \(2 v\) respectively as shown in the figure between collisions, the particles move with constant speeds. After making how many elastic collision other than that at \(A\). These two particles will again reach the point \(A\)
355279
Assertion :
\(n\) small balls (per second) (each of mass \(m\) ) are colliding elastically with vertical surface with velocity \(u\). The force experienced by the surface is \(2\,mnu\).
Reason :
On elastic collision, in this case, the ball rebounds with the same velocity.
355280 A particle of mass \(m\) moves towards a smooth vertical wall with a speed \(u\) (relative to the ground) and collides elastically with the wall, the wall moving towards the particle with a speed 2 \(u\) (also relative to the ground). Assuming that the wall is extremely massive, the impulse delivered to the particle equals.