355247
A particle of mass \(m\) strikes elastically with a disc of radius \(R\), with a velocity \(\vec{v}\) as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, then the velocity of the disc just after the collision is :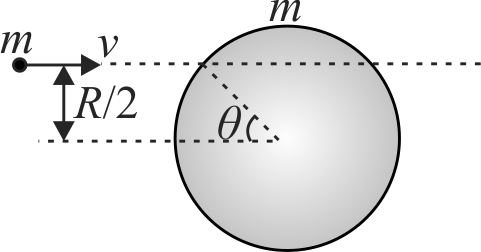
355248
In the figure shown, the two identical balls of mass \(M\) and radius \(R\) each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass \(M\) and radius \(R\), is coming down vertically and has a velocity \(v_{0}\) when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to: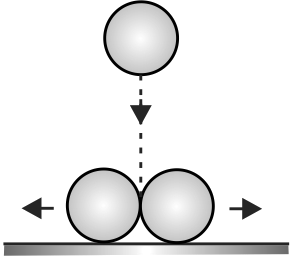
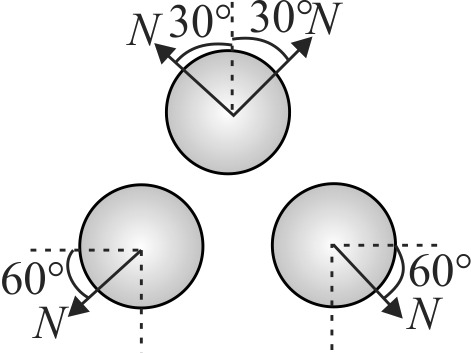
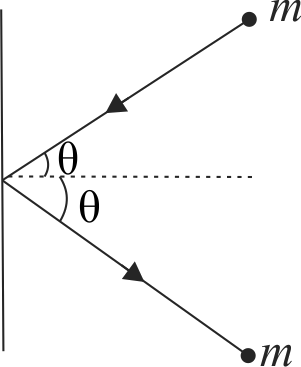
355251 Two particles \(A\) and \(B\) of masses \(3\;kg\) and \(6\;kg\) respectively, are incident making angles \(45^{\circ}\) and \(120^{\circ}\) with a same normal. These particles moving with speeds \(8\;m{\rm{/}}s\) and \(6\;m{\rm{/}}s,\) collide elastically at the origin. After the collision, particle \(B\) moves with a speed of (Take \(\sqrt{2}=1.41\) and \(\sqrt{3}=1.73\) )
355247
A particle of mass \(m\) strikes elastically with a disc of radius \(R\), with a velocity \(\vec{v}\) as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, then the velocity of the disc just after the collision is :
355248
In the figure shown, the two identical balls of mass \(M\) and radius \(R\) each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass \(M\) and radius \(R\), is coming down vertically and has a velocity \(v_{0}\) when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to:
355251 Two particles \(A\) and \(B\) of masses \(3\;kg\) and \(6\;kg\) respectively, are incident making angles \(45^{\circ}\) and \(120^{\circ}\) with a same normal. These particles moving with speeds \(8\;m{\rm{/}}s\) and \(6\;m{\rm{/}}s,\) collide elastically at the origin. After the collision, particle \(B\) moves with a speed of (Take \(\sqrt{2}=1.41\) and \(\sqrt{3}=1.73\) )
355247
A particle of mass \(m\) strikes elastically with a disc of radius \(R\), with a velocity \(\vec{v}\) as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, then the velocity of the disc just after the collision is :
355248
In the figure shown, the two identical balls of mass \(M\) and radius \(R\) each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass \(M\) and radius \(R\), is coming down vertically and has a velocity \(v_{0}\) when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to:
355251 Two particles \(A\) and \(B\) of masses \(3\;kg\) and \(6\;kg\) respectively, are incident making angles \(45^{\circ}\) and \(120^{\circ}\) with a same normal. These particles moving with speeds \(8\;m{\rm{/}}s\) and \(6\;m{\rm{/}}s,\) collide elastically at the origin. After the collision, particle \(B\) moves with a speed of (Take \(\sqrt{2}=1.41\) and \(\sqrt{3}=1.73\) )
355247
A particle of mass \(m\) strikes elastically with a disc of radius \(R\), with a velocity \(\vec{v}\) as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, then the velocity of the disc just after the collision is :
355248
In the figure shown, the two identical balls of mass \(M\) and radius \(R\) each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass \(M\) and radius \(R\), is coming down vertically and has a velocity \(v_{0}\) when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to:
355251 Two particles \(A\) and \(B\) of masses \(3\;kg\) and \(6\;kg\) respectively, are incident making angles \(45^{\circ}\) and \(120^{\circ}\) with a same normal. These particles moving with speeds \(8\;m{\rm{/}}s\) and \(6\;m{\rm{/}}s,\) collide elastically at the origin. After the collision, particle \(B\) moves with a speed of (Take \(\sqrt{2}=1.41\) and \(\sqrt{3}=1.73\) )
355247
A particle of mass \(m\) strikes elastically with a disc of radius \(R\), with a velocity \(\vec{v}\) as shown in the figure. If the mass of the disc is equal to that of the particle and the surface of the contact is smooth, then the velocity of the disc just after the collision is :
355248
In the figure shown, the two identical balls of mass \(M\) and radius \(R\) each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass \(M\) and radius \(R\), is coming down vertically and has a velocity \(v_{0}\) when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to:
355251 Two particles \(A\) and \(B\) of masses \(3\;kg\) and \(6\;kg\) respectively, are incident making angles \(45^{\circ}\) and \(120^{\circ}\) with a same normal. These particles moving with speeds \(8\;m{\rm{/}}s\) and \(6\;m{\rm{/}}s,\) collide elastically at the origin. After the collision, particle \(B\) moves with a speed of (Take \(\sqrt{2}=1.41\) and \(\sqrt{3}=1.73\) )