355173
An object of mass \(m\) is hung from a thin taut string (with linear mass density \(\mu=2 {~g} / {m}\) ) that passes over a light pulley as shown in figure. The string is connected to a vibrator which can be vibrated with constant frequency \(f\), and the length of the string between vibrator and the pulley is \(L=2.0 {~m}\). The standing waves are formed when the mass \(m\) of the object is either 16.0 \(kg\) or 25.0 \(kg\) . It is observed that no standing waves are formed with any mass between these values, however. What is the largest object mass for which standing waves could be observed? (Use \(g=9.8 {~m} / {s}^{2}\) )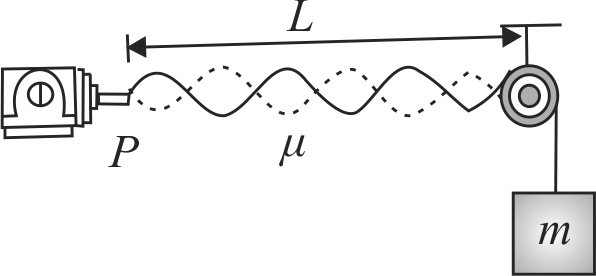
355175 A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by \(y(x, t)=0.5 \sin \left(\dfrac{5 \pi}{4} x\right) \cos (200 \pi t)\) What is the speed of the travelling wave moving in the positive \(x\) direction ? \(x\)and \(t\) are in meter and second, respectively.)
355173
An object of mass \(m\) is hung from a thin taut string (with linear mass density \(\mu=2 {~g} / {m}\) ) that passes over a light pulley as shown in figure. The string is connected to a vibrator which can be vibrated with constant frequency \(f\), and the length of the string between vibrator and the pulley is \(L=2.0 {~m}\). The standing waves are formed when the mass \(m\) of the object is either 16.0 \(kg\) or 25.0 \(kg\) . It is observed that no standing waves are formed with any mass between these values, however. What is the largest object mass for which standing waves could be observed? (Use \(g=9.8 {~m} / {s}^{2}\) )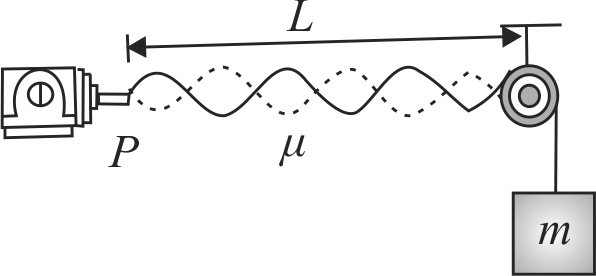
355175 A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by \(y(x, t)=0.5 \sin \left(\dfrac{5 \pi}{4} x\right) \cos (200 \pi t)\) What is the speed of the travelling wave moving in the positive \(x\) direction ? \(x\)and \(t\) are in meter and second, respectively.)
355173
An object of mass \(m\) is hung from a thin taut string (with linear mass density \(\mu=2 {~g} / {m}\) ) that passes over a light pulley as shown in figure. The string is connected to a vibrator which can be vibrated with constant frequency \(f\), and the length of the string between vibrator and the pulley is \(L=2.0 {~m}\). The standing waves are formed when the mass \(m\) of the object is either 16.0 \(kg\) or 25.0 \(kg\) . It is observed that no standing waves are formed with any mass between these values, however. What is the largest object mass for which standing waves could be observed? (Use \(g=9.8 {~m} / {s}^{2}\) )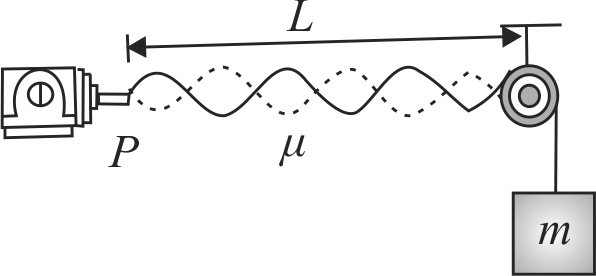
355175 A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by \(y(x, t)=0.5 \sin \left(\dfrac{5 \pi}{4} x\right) \cos (200 \pi t)\) What is the speed of the travelling wave moving in the positive \(x\) direction ? \(x\)and \(t\) are in meter and second, respectively.)
355173
An object of mass \(m\) is hung from a thin taut string (with linear mass density \(\mu=2 {~g} / {m}\) ) that passes over a light pulley as shown in figure. The string is connected to a vibrator which can be vibrated with constant frequency \(f\), and the length of the string between vibrator and the pulley is \(L=2.0 {~m}\). The standing waves are formed when the mass \(m\) of the object is either 16.0 \(kg\) or 25.0 \(kg\) . It is observed that no standing waves are formed with any mass between these values, however. What is the largest object mass for which standing waves could be observed? (Use \(g=9.8 {~m} / {s}^{2}\) )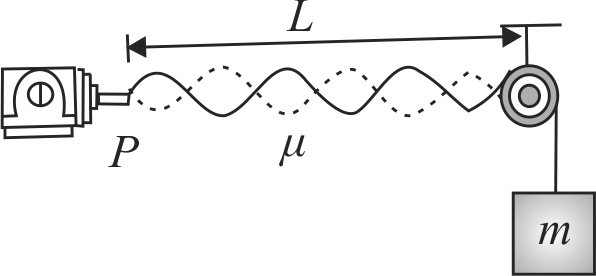
355175 A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by \(y(x, t)=0.5 \sin \left(\dfrac{5 \pi}{4} x\right) \cos (200 \pi t)\) What is the speed of the travelling wave moving in the positive \(x\) direction ? \(x\)and \(t\) are in meter and second, respectively.)
