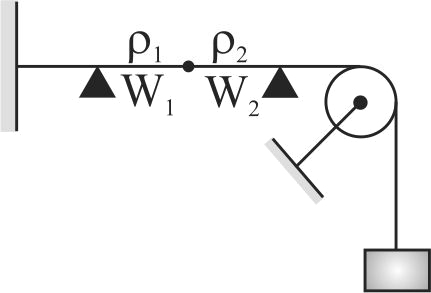355113 Two wires are fixed on a sonometer wire. Their tensions are in the ratio \(8: 1\), the lengths in the ratio \(36: 35\), the diameters in the ratio \(4: 1\) and the densities in the ratio \(1: 2\). Find the frequency of the beats produced if the note of the higher pitch has frequency of 360 \(Hz\) .
355114
Two wires \(W_{1}\) and \(W_{2}\) have the same radius \(r\) and respective densities \(\rho_{1}\) and \(\rho_{2}\) such that \(\rho_{2}=4 \rho_{1}\). They are joined together at the point \(O\), as shown in the figure. The combination is used as a sonometer wire and kept under tension \(T\). The point \(O\) is midway between the bridges. When a stationary waves is set up in the composite wire, the joint is formed to be a node. The ratio of the number of antinodes formed in \(W_{1}\) to \(W_{2}\) is :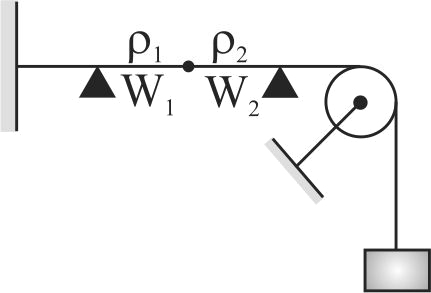
355113 Two wires are fixed on a sonometer wire. Their tensions are in the ratio \(8: 1\), the lengths in the ratio \(36: 35\), the diameters in the ratio \(4: 1\) and the densities in the ratio \(1: 2\). Find the frequency of the beats produced if the note of the higher pitch has frequency of 360 \(Hz\) .
355114
Two wires \(W_{1}\) and \(W_{2}\) have the same radius \(r\) and respective densities \(\rho_{1}\) and \(\rho_{2}\) such that \(\rho_{2}=4 \rho_{1}\). They are joined together at the point \(O\), as shown in the figure. The combination is used as a sonometer wire and kept under tension \(T\). The point \(O\) is midway between the bridges. When a stationary waves is set up in the composite wire, the joint is formed to be a node. The ratio of the number of antinodes formed in \(W_{1}\) to \(W_{2}\) is :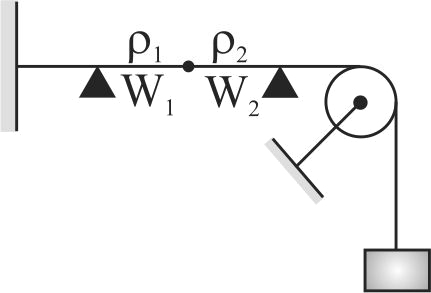
355113 Two wires are fixed on a sonometer wire. Their tensions are in the ratio \(8: 1\), the lengths in the ratio \(36: 35\), the diameters in the ratio \(4: 1\) and the densities in the ratio \(1: 2\). Find the frequency of the beats produced if the note of the higher pitch has frequency of 360 \(Hz\) .
355114
Two wires \(W_{1}\) and \(W_{2}\) have the same radius \(r\) and respective densities \(\rho_{1}\) and \(\rho_{2}\) such that \(\rho_{2}=4 \rho_{1}\). They are joined together at the point \(O\), as shown in the figure. The combination is used as a sonometer wire and kept under tension \(T\). The point \(O\) is midway between the bridges. When a stationary waves is set up in the composite wire, the joint is formed to be a node. The ratio of the number of antinodes formed in \(W_{1}\) to \(W_{2}\) is :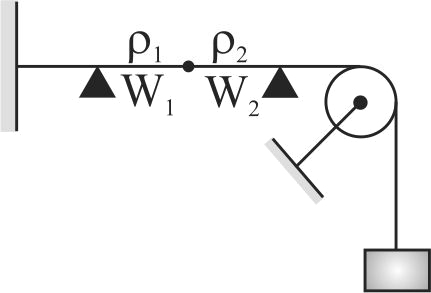
355113 Two wires are fixed on a sonometer wire. Their tensions are in the ratio \(8: 1\), the lengths in the ratio \(36: 35\), the diameters in the ratio \(4: 1\) and the densities in the ratio \(1: 2\). Find the frequency of the beats produced if the note of the higher pitch has frequency of 360 \(Hz\) .
355114
Two wires \(W_{1}\) and \(W_{2}\) have the same radius \(r\) and respective densities \(\rho_{1}\) and \(\rho_{2}\) such that \(\rho_{2}=4 \rho_{1}\). They are joined together at the point \(O\), as shown in the figure. The combination is used as a sonometer wire and kept under tension \(T\). The point \(O\) is midway between the bridges. When a stationary waves is set up in the composite wire, the joint is formed to be a node. The ratio of the number of antinodes formed in \(W_{1}\) to \(W_{2}\) is :