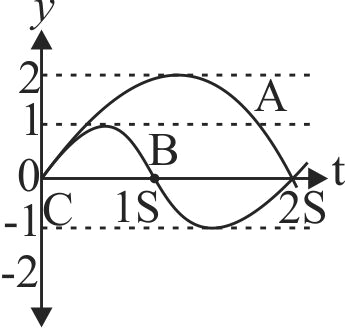
355070 Two waves of nearly same amplitude, same frequency travelling with same velocity are superimposing to give phenomenon of interference. If \(a_{1}\) and \(a_{2}\) be their amplitudes, \(\omega\) be the frequency for both, \(v\) be the velocity for both and \(\Delta \phi\) is the phase difference between the two waves then, incorrect statement among the following
355072
Assertion :
Velocity of particles, while crossing mean position (in stationary waves) varies from maximum at antinodes to zero at nodes.
Reason :
Amplitude of vibration at antinodes is maximum and at nodes, the amplitude is zero, and all particles between two successive nodes cross the mean position together.
355070 Two waves of nearly same amplitude, same frequency travelling with same velocity are superimposing to give phenomenon of interference. If \(a_{1}\) and \(a_{2}\) be their amplitudes, \(\omega\) be the frequency for both, \(v\) be the velocity for both and \(\Delta \phi\) is the phase difference between the two waves then, incorrect statement among the following
355072
Assertion :
Velocity of particles, while crossing mean position (in stationary waves) varies from maximum at antinodes to zero at nodes.
Reason :
Amplitude of vibration at antinodes is maximum and at nodes, the amplitude is zero, and all particles between two successive nodes cross the mean position together.
355070 Two waves of nearly same amplitude, same frequency travelling with same velocity are superimposing to give phenomenon of interference. If \(a_{1}\) and \(a_{2}\) be their amplitudes, \(\omega\) be the frequency for both, \(v\) be the velocity for both and \(\Delta \phi\) is the phase difference between the two waves then, incorrect statement among the following
355072
Assertion :
Velocity of particles, while crossing mean position (in stationary waves) varies from maximum at antinodes to zero at nodes.
Reason :
Amplitude of vibration at antinodes is maximum and at nodes, the amplitude is zero, and all particles between two successive nodes cross the mean position together.
355070 Two waves of nearly same amplitude, same frequency travelling with same velocity are superimposing to give phenomenon of interference. If \(a_{1}\) and \(a_{2}\) be their amplitudes, \(\omega\) be the frequency for both, \(v\) be the velocity for both and \(\Delta \phi\) is the phase difference between the two waves then, incorrect statement among the following
355072
Assertion :
Velocity of particles, while crossing mean position (in stationary waves) varies from maximum at antinodes to zero at nodes.
Reason :
Amplitude of vibration at antinodes is maximum and at nodes, the amplitude is zero, and all particles between two successive nodes cross the mean position together.
355070 Two waves of nearly same amplitude, same frequency travelling with same velocity are superimposing to give phenomenon of interference. If \(a_{1}\) and \(a_{2}\) be their amplitudes, \(\omega\) be the frequency for both, \(v\) be the velocity for both and \(\Delta \phi\) is the phase difference between the two waves then, incorrect statement among the following
355072
Assertion :
Velocity of particles, while crossing mean position (in stationary waves) varies from maximum at antinodes to zero at nodes.
Reason :
Amplitude of vibration at antinodes is maximum and at nodes, the amplitude is zero, and all particles between two successive nodes cross the mean position together.