355065
Two metallic strings \(A\) and \(B\) of different materials are connected in series forming a joint. The strings have similar cross-sectional area \(a=1 {~mm}^{2}\). The length of \(A\) is \(l_{A}=0.3 {~m}\) and that \(B\) is \(l_{B}=0.75 {~m}\). One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass \(m=25.2 {~kg}\) passing over a frictionless pulley. Transverse waves are set up in the combined string using an external source of variable frequency, calculate the lowest frequency for which standing waves are observed such that the joint is a node.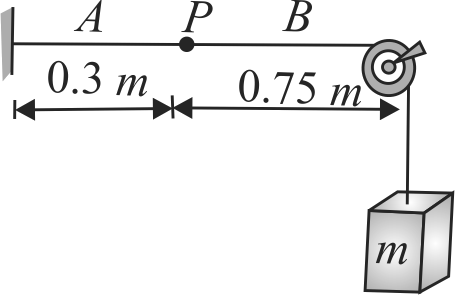
The densities of \(A\) and \(B\) are \(6.3 \times 10^{3} {~kg} / {m}^{3}\) and \(2.8 \times 10^{3} {~kg} / {m}\) respectively.
355065
Two metallic strings \(A\) and \(B\) of different materials are connected in series forming a joint. The strings have similar cross-sectional area \(a=1 {~mm}^{2}\). The length of \(A\) is \(l_{A}=0.3 {~m}\) and that \(B\) is \(l_{B}=0.75 {~m}\). One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass \(m=25.2 {~kg}\) passing over a frictionless pulley. Transverse waves are set up in the combined string using an external source of variable frequency, calculate the lowest frequency for which standing waves are observed such that the joint is a node.
The densities of \(A\) and \(B\) are \(6.3 \times 10^{3} {~kg} / {m}^{3}\) and \(2.8 \times 10^{3} {~kg} / {m}\) respectively.
355065
Two metallic strings \(A\) and \(B\) of different materials are connected in series forming a joint. The strings have similar cross-sectional area \(a=1 {~mm}^{2}\). The length of \(A\) is \(l_{A}=0.3 {~m}\) and that \(B\) is \(l_{B}=0.75 {~m}\). One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass \(m=25.2 {~kg}\) passing over a frictionless pulley. Transverse waves are set up in the combined string using an external source of variable frequency, calculate the lowest frequency for which standing waves are observed such that the joint is a node.
The densities of \(A\) and \(B\) are \(6.3 \times 10^{3} {~kg} / {m}^{3}\) and \(2.8 \times 10^{3} {~kg} / {m}\) respectively.
355065
Two metallic strings \(A\) and \(B\) of different materials are connected in series forming a joint. The strings have similar cross-sectional area \(a=1 {~mm}^{2}\). The length of \(A\) is \(l_{A}=0.3 {~m}\) and that \(B\) is \(l_{B}=0.75 {~m}\). One end of the combined string is tied with a support rigidly and the other end is loaded with a block of mass \(m=25.2 {~kg}\) passing over a frictionless pulley. Transverse waves are set up in the combined string using an external source of variable frequency, calculate the lowest frequency for which standing waves are observed such that the joint is a node.
The densities of \(A\) and \(B\) are \(6.3 \times 10^{3} {~kg} / {m}^{3}\) and \(2.8 \times 10^{3} {~kg} / {m}\) respectively.