Explanation:
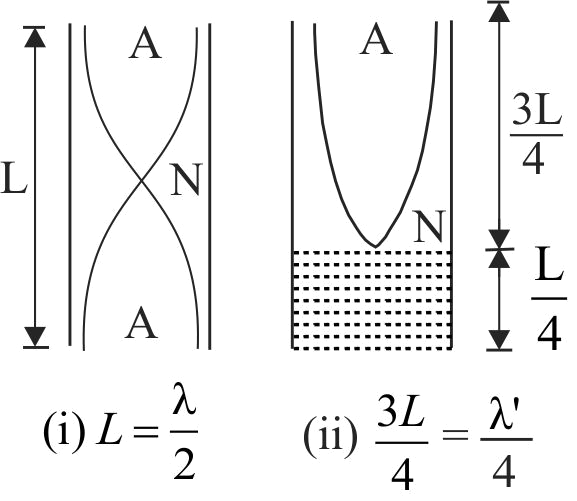
For a cylindrical tube open at both ends, its fundamental frequency is
\(f = \frac{v}{\lambda } = \frac{v}{{2L}} = 390\;Hz\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
where \(v\) is the velocity of sound in air.
If \((1 / 4)^{\text {th }}\) of cylindrical tube is immersed in a water, it will become a closed pipe of length three fourth that of an open pipe as shown in figure (ii). Therefore, its fundamental
frequency is
\({f^\prime } = \frac{v}{{{\lambda ^\prime }}} = \frac{v}{{\left( {4 \times \frac{3}{4}\;L} \right)}}\,\)
\( \Rightarrow {f^\prime } = \frac{v}{{3L}} = \frac{2}{3}\left( {\frac{v}{{2L}}} \right) = \frac{2}{3} \times 390\;Hz\) [using eq. (1)]
\( = 260\;Hz.\)