354920 A pipe closed at one end has length \(83\;cm\). The number of possible natural oscillations of air column whose frequencies lie below \(1000\;Hz\) are ( take, velocity of sound in air \( = 332\;m/s\))

354921 A closed organ pipe has length ' \(l\) '. The air in it is vibrating in \(3^{\text {rd }}\) overtone with maximum displacement amplitude \(a\). The displacement amplitude at a distance of \(\dfrac{l}{7}\) from closed end of the pipe is equal to

354922 The waves set up in a closed pipe are

354923 A source of sound placed at the open end of a resonance column sends an acoustic wave of pressure amplitude \(P_{0}\) inside the tube. If the atmospheric pressure is \(P_{A}\), then the ratio of maximum and minimum pressure at the closed end of the tube will be

354924 In a resonance tube experiment, a closed organ pipe of length \(120\;cm\) is used and tuned with a tuning fork of frequency \(340\;Hz\). If water is poured into the pipe, then incorrect statement among the following [velocity of sound in air is \(340\;m/s\), neglect end correction]

354920 A pipe closed at one end has length \(83\;cm\). The number of possible natural oscillations of air column whose frequencies lie below \(1000\;Hz\) are ( take, velocity of sound in air \( = 332\;m/s\))

354921 A closed organ pipe has length ' \(l\) '. The air in it is vibrating in \(3^{\text {rd }}\) overtone with maximum displacement amplitude \(a\). The displacement amplitude at a distance of \(\dfrac{l}{7}\) from closed end of the pipe is equal to

354922 The waves set up in a closed pipe are

354923 A source of sound placed at the open end of a resonance column sends an acoustic wave of pressure amplitude \(P_{0}\) inside the tube. If the atmospheric pressure is \(P_{A}\), then the ratio of maximum and minimum pressure at the closed end of the tube will be

354924 In a resonance tube experiment, a closed organ pipe of length \(120\;cm\) is used and tuned with a tuning fork of frequency \(340\;Hz\). If water is poured into the pipe, then incorrect statement among the following [velocity of sound in air is \(340\;m/s\), neglect end correction]

354920 A pipe closed at one end has length \(83\;cm\). The number of possible natural oscillations of air column whose frequencies lie below \(1000\;Hz\) are ( take, velocity of sound in air \( = 332\;m/s\))

354921 A closed organ pipe has length ' \(l\) '. The air in it is vibrating in \(3^{\text {rd }}\) overtone with maximum displacement amplitude \(a\). The displacement amplitude at a distance of \(\dfrac{l}{7}\) from closed end of the pipe is equal to

354922 The waves set up in a closed pipe are

354923 A source of sound placed at the open end of a resonance column sends an acoustic wave of pressure amplitude \(P_{0}\) inside the tube. If the atmospheric pressure is \(P_{A}\), then the ratio of maximum and minimum pressure at the closed end of the tube will be

354924 In a resonance tube experiment, a closed organ pipe of length \(120\;cm\) is used and tuned with a tuning fork of frequency \(340\;Hz\). If water is poured into the pipe, then incorrect statement among the following [velocity of sound in air is \(340\;m/s\), neglect end correction]

354920 A pipe closed at one end has length \(83\;cm\). The number of possible natural oscillations of air column whose frequencies lie below \(1000\;Hz\) are ( take, velocity of sound in air \( = 332\;m/s\))

354921 A closed organ pipe has length ' \(l\) '. The air in it is vibrating in \(3^{\text {rd }}\) overtone with maximum displacement amplitude \(a\). The displacement amplitude at a distance of \(\dfrac{l}{7}\) from closed end of the pipe is equal to

354922 The waves set up in a closed pipe are

354923 A source of sound placed at the open end of a resonance column sends an acoustic wave of pressure amplitude \(P_{0}\) inside the tube. If the atmospheric pressure is \(P_{A}\), then the ratio of maximum and minimum pressure at the closed end of the tube will be

354924 In a resonance tube experiment, a closed organ pipe of length \(120\;cm\) is used and tuned with a tuning fork of frequency \(340\;Hz\). If water is poured into the pipe, then incorrect statement among the following [velocity of sound in air is \(340\;m/s\), neglect end correction]

354920 A pipe closed at one end has length \(83\;cm\). The number of possible natural oscillations of air column whose frequencies lie below \(1000\;Hz\) are ( take, velocity of sound in air \( = 332\;m/s\))

354921 A closed organ pipe has length ' \(l\) '. The air in it is vibrating in \(3^{\text {rd }}\) overtone with maximum displacement amplitude \(a\). The displacement amplitude at a distance of \(\dfrac{l}{7}\) from closed end of the pipe is equal to

354922 The waves set up in a closed pipe are

354923 A source of sound placed at the open end of a resonance column sends an acoustic wave of pressure amplitude \(P_{0}\) inside the tube. If the atmospheric pressure is \(P_{A}\), then the ratio of maximum and minimum pressure at the closed end of the tube will be

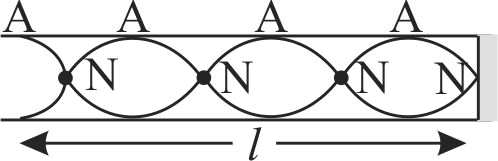
354924 In a resonance tube experiment, a closed organ pipe of length \(120\;cm\) is used and tuned with a tuning fork of frequency \(340\;Hz\). If water is poured into the pipe, then incorrect statement among the following [velocity of sound in air is \(340\;m/s\), neglect end correction]