354849
The transverse displacement of a string (clamped at its both ends) is given by
\({y(x, t)=0.6 \sin \left(\dfrac{2 \pi}{3} x\right) \cos (120 \pi t)}\)
where \({x}\) and \({y}\) are in metre and \({t}\) is in second. If the length of the string is \(1.5\,m\) and its mass is \({3.0 \times 10^{-2} {~kg}}\), the tension in the string will be
354850
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of \(45\;Hz\). The mass of the wire is \(3.5 \times {10^{ - 2}}\;kg\) and its linear mass density is \(4.0 \times {10^{ - 2}}\;kg/m\). What is
(i) the speed of a transverse wave on the string and
(ii) the tension in the string?
354851
A "Tsunami" that is huge tidal wave is created at \(O\) of the ocean and travelled towards shore as shown. It was found that the amplitude of wave \(A\) is inversely proportional to \({h^{1/4}},\;h\) is height of water surface from bed. If the wave amplitude at the open sea having depth \(4.3\;km\) is \(0.5\;cm\), then the amplitude at coastal shallows having depth \(10\;m\) is \(0.2 x\) meter. The value of \(x\) is____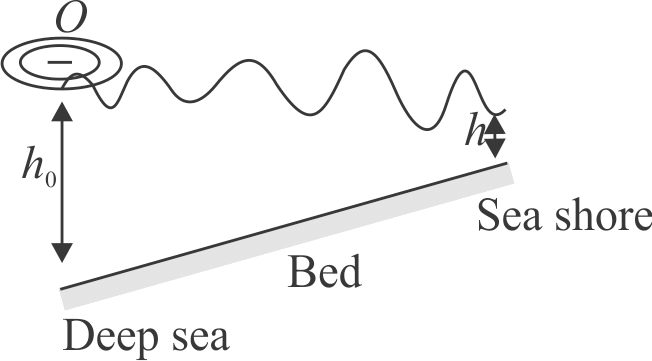
354849
The transverse displacement of a string (clamped at its both ends) is given by
\({y(x, t)=0.6 \sin \left(\dfrac{2 \pi}{3} x\right) \cos (120 \pi t)}\)
where \({x}\) and \({y}\) are in metre and \({t}\) is in second. If the length of the string is \(1.5\,m\) and its mass is \({3.0 \times 10^{-2} {~kg}}\), the tension in the string will be
354850
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of \(45\;Hz\). The mass of the wire is \(3.5 \times {10^{ - 2}}\;kg\) and its linear mass density is \(4.0 \times {10^{ - 2}}\;kg/m\). What is
(i) the speed of a transverse wave on the string and
(ii) the tension in the string?
354851
A "Tsunami" that is huge tidal wave is created at \(O\) of the ocean and travelled towards shore as shown. It was found that the amplitude of wave \(A\) is inversely proportional to \({h^{1/4}},\;h\) is height of water surface from bed. If the wave amplitude at the open sea having depth \(4.3\;km\) is \(0.5\;cm\), then the amplitude at coastal shallows having depth \(10\;m\) is \(0.2 x\) meter. The value of \(x\) is____
354849
The transverse displacement of a string (clamped at its both ends) is given by
\({y(x, t)=0.6 \sin \left(\dfrac{2 \pi}{3} x\right) \cos (120 \pi t)}\)
where \({x}\) and \({y}\) are in metre and \({t}\) is in second. If the length of the string is \(1.5\,m\) and its mass is \({3.0 \times 10^{-2} {~kg}}\), the tension in the string will be
354850
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of \(45\;Hz\). The mass of the wire is \(3.5 \times {10^{ - 2}}\;kg\) and its linear mass density is \(4.0 \times {10^{ - 2}}\;kg/m\). What is
(i) the speed of a transverse wave on the string and
(ii) the tension in the string?
354851
A "Tsunami" that is huge tidal wave is created at \(O\) of the ocean and travelled towards shore as shown. It was found that the amplitude of wave \(A\) is inversely proportional to \({h^{1/4}},\;h\) is height of water surface from bed. If the wave amplitude at the open sea having depth \(4.3\;km\) is \(0.5\;cm\), then the amplitude at coastal shallows having depth \(10\;m\) is \(0.2 x\) meter. The value of \(x\) is____
354849
The transverse displacement of a string (clamped at its both ends) is given by
\({y(x, t)=0.6 \sin \left(\dfrac{2 \pi}{3} x\right) \cos (120 \pi t)}\)
where \({x}\) and \({y}\) are in metre and \({t}\) is in second. If the length of the string is \(1.5\,m\) and its mass is \({3.0 \times 10^{-2} {~kg}}\), the tension in the string will be
354850
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of \(45\;Hz\). The mass of the wire is \(3.5 \times {10^{ - 2}}\;kg\) and its linear mass density is \(4.0 \times {10^{ - 2}}\;kg/m\). What is
(i) the speed of a transverse wave on the string and
(ii) the tension in the string?
354851
A "Tsunami" that is huge tidal wave is created at \(O\) of the ocean and travelled towards shore as shown. It was found that the amplitude of wave \(A\) is inversely proportional to \({h^{1/4}},\;h\) is height of water surface from bed. If the wave amplitude at the open sea having depth \(4.3\;km\) is \(0.5\;cm\), then the amplitude at coastal shallows having depth \(10\;m\) is \(0.2 x\) meter. The value of \(x\) is____
354849
The transverse displacement of a string (clamped at its both ends) is given by
\({y(x, t)=0.6 \sin \left(\dfrac{2 \pi}{3} x\right) \cos (120 \pi t)}\)
where \({x}\) and \({y}\) are in metre and \({t}\) is in second. If the length of the string is \(1.5\,m\) and its mass is \({3.0 \times 10^{-2} {~kg}}\), the tension in the string will be
354850
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of \(45\;Hz\). The mass of the wire is \(3.5 \times {10^{ - 2}}\;kg\) and its linear mass density is \(4.0 \times {10^{ - 2}}\;kg/m\). What is
(i) the speed of a transverse wave on the string and
(ii) the tension in the string?
354851
A "Tsunami" that is huge tidal wave is created at \(O\) of the ocean and travelled towards shore as shown. It was found that the amplitude of wave \(A\) is inversely proportional to \({h^{1/4}},\;h\) is height of water surface from bed. If the wave amplitude at the open sea having depth \(4.3\;km\) is \(0.5\;cm\), then the amplitude at coastal shallows having depth \(10\;m\) is \(0.2 x\) meter. The value of \(x\) is____