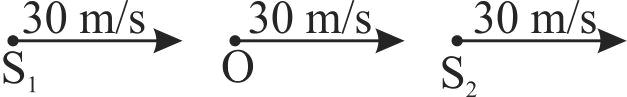354750 The observer is moving with velocity ' \(v_{0}\) ' towards the stationary source of sound and then after crossing moves away from the source with velocity \(v_{0}\). Assume that the medium through which the sound wave travel is at rest. If \(v\) is velocity of sound and \(n\) is the frequency emitted by the source, then the difference between apparent frequencies heard by the observer is
354750 The observer is moving with velocity ' \(v_{0}\) ' towards the stationary source of sound and then after crossing moves away from the source with velocity \(v_{0}\). Assume that the medium through which the sound wave travel is at rest. If \(v\) is velocity of sound and \(n\) is the frequency emitted by the source, then the difference between apparent frequencies heard by the observer is
354750 The observer is moving with velocity ' \(v_{0}\) ' towards the stationary source of sound and then after crossing moves away from the source with velocity \(v_{0}\). Assume that the medium through which the sound wave travel is at rest. If \(v\) is velocity of sound and \(n\) is the frequency emitted by the source, then the difference between apparent frequencies heard by the observer is
354750 The observer is moving with velocity ' \(v_{0}\) ' towards the stationary source of sound and then after crossing moves away from the source with velocity \(v_{0}\). Assume that the medium through which the sound wave travel is at rest. If \(v\) is velocity of sound and \(n\) is the frequency emitted by the source, then the difference between apparent frequencies heard by the observer is