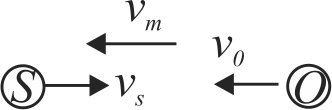354724 A source of sound \(S\) is moving with a velocity of \(50\;m{s^{ - 1}}\) towards a stationary observer. The observer measures the frequency of the source as \(1000\;Hz\). What will be the apparent frequency of the sound has heard by observer when the source is moving away from the observer after crossing him? (the velocity of the sound in the medium is \(350\;m{s^{ - 1}}\) ).
354725 Velocity of sound is \(v\). Source and observer move towards each other with velocities \(v_{s}\) and \(v_{0}\) respectively. Wind is blowing with a velocity \(v_{m}\) in the direction opposite to the propagation of sound; \(n\) is the pitch of the sound. The apparent pitch of the sound heard by the observer is
354724 A source of sound \(S\) is moving with a velocity of \(50\;m{s^{ - 1}}\) towards a stationary observer. The observer measures the frequency of the source as \(1000\;Hz\). What will be the apparent frequency of the sound has heard by observer when the source is moving away from the observer after crossing him? (the velocity of the sound in the medium is \(350\;m{s^{ - 1}}\) ).
354725 Velocity of sound is \(v\). Source and observer move towards each other with velocities \(v_{s}\) and \(v_{0}\) respectively. Wind is blowing with a velocity \(v_{m}\) in the direction opposite to the propagation of sound; \(n\) is the pitch of the sound. The apparent pitch of the sound heard by the observer is
354724 A source of sound \(S\) is moving with a velocity of \(50\;m{s^{ - 1}}\) towards a stationary observer. The observer measures the frequency of the source as \(1000\;Hz\). What will be the apparent frequency of the sound has heard by observer when the source is moving away from the observer after crossing him? (the velocity of the sound in the medium is \(350\;m{s^{ - 1}}\) ).
354725 Velocity of sound is \(v\). Source and observer move towards each other with velocities \(v_{s}\) and \(v_{0}\) respectively. Wind is blowing with a velocity \(v_{m}\) in the direction opposite to the propagation of sound; \(n\) is the pitch of the sound. The apparent pitch of the sound heard by the observer is
354724 A source of sound \(S\) is moving with a velocity of \(50\;m{s^{ - 1}}\) towards a stationary observer. The observer measures the frequency of the source as \(1000\;Hz\). What will be the apparent frequency of the sound has heard by observer when the source is moving away from the observer after crossing him? (the velocity of the sound in the medium is \(350\;m{s^{ - 1}}\) ).
354725 Velocity of sound is \(v\). Source and observer move towards each other with velocities \(v_{s}\) and \(v_{0}\) respectively. Wind is blowing with a velocity \(v_{m}\) in the direction opposite to the propagation of sound; \(n\) is the pitch of the sound. The apparent pitch of the sound heard by the observer is
354724 A source of sound \(S\) is moving with a velocity of \(50\;m{s^{ - 1}}\) towards a stationary observer. The observer measures the frequency of the source as \(1000\;Hz\). What will be the apparent frequency of the sound has heard by observer when the source is moving away from the observer after crossing him? (the velocity of the sound in the medium is \(350\;m{s^{ - 1}}\) ).
354725 Velocity of sound is \(v\). Source and observer move towards each other with velocities \(v_{s}\) and \(v_{0}\) respectively. Wind is blowing with a velocity \(v_{m}\) in the direction opposite to the propagation of sound; \(n\) is the pitch of the sound. The apparent pitch of the sound heard by the observer is