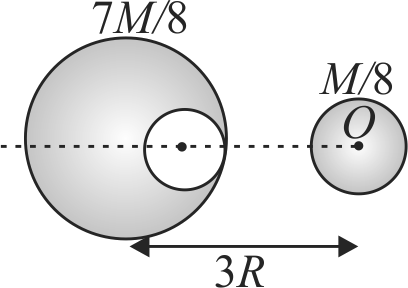
360014 From a sphere of mass \(M\) and radius \(R\), a smaller sphere of radius \(\frac{R}{2}\) is carved out such that the cavity made in the original sphere is between its centre and the periphery. (See figure). For the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is 3\(R\), the gravitational force between the two spheres is :-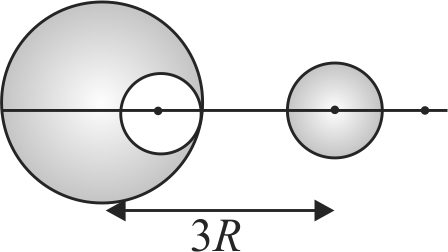

360015 Newton's universal law of gravitation applies to

360016 The magnitude of the force of gravity between two identical objects is given by \(F_{0}\). If the mass of each object is doubled but the distance between them is halved, then the new force of
gravity between the objects will be:

360017 Four similar particles of mass \(m\) are orbiting in a circular of radius \(r\) in the same angular direction because of their mutual gravitational attractive force. The angular velocity of a particle is given by

360014 From a sphere of mass \(M\) and radius \(R\), a smaller sphere of radius \(\frac{R}{2}\) is carved out such that the cavity made in the original sphere is between its centre and the periphery. (See figure). For the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is 3\(R\), the gravitational force between the two spheres is :-

360015 Newton's universal law of gravitation applies to

360016 The magnitude of the force of gravity between two identical objects is given by \(F_{0}\). If the mass of each object is doubled but the distance between them is halved, then the new force of
gravity between the objects will be:

360017 Four similar particles of mass \(m\) are orbiting in a circular of radius \(r\) in the same angular direction because of their mutual gravitational attractive force. The angular velocity of a particle is given by

360014 From a sphere of mass \(M\) and radius \(R\), a smaller sphere of radius \(\frac{R}{2}\) is carved out such that the cavity made in the original sphere is between its centre and the periphery. (See figure). For the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is 3\(R\), the gravitational force between the two spheres is :-

360015 Newton's universal law of gravitation applies to

360016 The magnitude of the force of gravity between two identical objects is given by \(F_{0}\). If the mass of each object is doubled but the distance between them is halved, then the new force of
gravity between the objects will be:

360017 Four similar particles of mass \(m\) are orbiting in a circular of radius \(r\) in the same angular direction because of their mutual gravitational attractive force. The angular velocity of a particle is given by

360014 From a sphere of mass \(M\) and radius \(R\), a smaller sphere of radius \(\frac{R}{2}\) is carved out such that the cavity made in the original sphere is between its centre and the periphery. (See figure). For the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is 3\(R\), the gravitational force between the two spheres is :-

360015 Newton's universal law of gravitation applies to

360016 The magnitude of the force of gravity between two identical objects is given by \(F_{0}\). If the mass of each object is doubled but the distance between them is halved, then the new force of
gravity between the objects will be:

360017 Four similar particles of mass \(m\) are orbiting in a circular of radius \(r\) in the same angular direction because of their mutual gravitational attractive force. The angular velocity of a particle is given by