359937
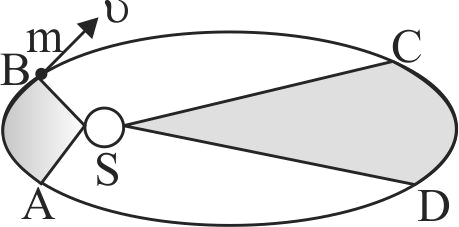
The figure shows elliptical orbit of a planet \(m\) about the sun \(S\). The shaded area \(SCD\) is twice the shaded area \(SAB\). If \(t_{1}\) is the time for the planet to move from \(C\) to \(D\) and \(t_{2}\) is the time to move from \(A\) to \(B\), then:
 { width: 38.862mm; }
359940
Consider a satellite orbiting the earth as shown in the figure below. Let \(L_{a}\) and \(L_{p}\) represent the angular momentum of the satellite about the earth when at aphelion and perihelion, respectively. Consider the following relations,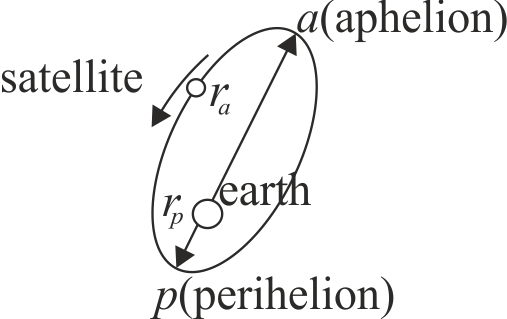
I. \(L_{a}=L_{p}\)
II. \(\mathrm{L}_{a}=-L_{p}\)
III. \(r_{a} \times L_{a}=r_{p} \times L_{p}\)
Which of the above relations is/are true?
359937
The figure shows elliptical orbit of a planet \(m\) about the sun \(S\). The shaded area \(SCD\) is twice the shaded area \(SAB\). If \(t_{1}\) is the time for the planet to move from \(C\) to \(D\) and \(t_{2}\) is the time to move from \(A\) to \(B\), then:
 { width: 38.862mm; }
359940
Consider a satellite orbiting the earth as shown in the figure below. Let \(L_{a}\) and \(L_{p}\) represent the angular momentum of the satellite about the earth when at aphelion and perihelion, respectively. Consider the following relations,
I. \(L_{a}=L_{p}\)
II. \(\mathrm{L}_{a}=-L_{p}\)
III. \(r_{a} \times L_{a}=r_{p} \times L_{p}\)
Which of the above relations is/are true?
359937
The figure shows elliptical orbit of a planet \(m\) about the sun \(S\). The shaded area \(SCD\) is twice the shaded area \(SAB\). If \(t_{1}\) is the time for the planet to move from \(C\) to \(D\) and \(t_{2}\) is the time to move from \(A\) to \(B\), then:
 { width: 38.862mm; }
359940
Consider a satellite orbiting the earth as shown in the figure below. Let \(L_{a}\) and \(L_{p}\) represent the angular momentum of the satellite about the earth when at aphelion and perihelion, respectively. Consider the following relations,
I. \(L_{a}=L_{p}\)
II. \(\mathrm{L}_{a}=-L_{p}\)
III. \(r_{a} \times L_{a}=r_{p} \times L_{p}\)
Which of the above relations is/are true?
359937
The figure shows elliptical orbit of a planet \(m\) about the sun \(S\). The shaded area \(SCD\) is twice the shaded area \(SAB\). If \(t_{1}\) is the time for the planet to move from \(C\) to \(D\) and \(t_{2}\) is the time to move from \(A\) to \(B\), then:
 { width: 38.862mm; }
359940
Consider a satellite orbiting the earth as shown in the figure below. Let \(L_{a}\) and \(L_{p}\) represent the angular momentum of the satellite about the earth when at aphelion and perihelion, respectively. Consider the following relations,
I. \(L_{a}=L_{p}\)
II. \(\mathrm{L}_{a}=-L_{p}\)
III. \(r_{a} \times L_{a}=r_{p} \times L_{p}\)
Which of the above relations is/are true?
